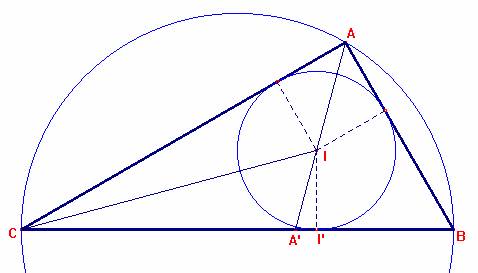
Problema 161

Sea ABC un triángulo rectángulo en A, que tiene la siguiente propiedad :
Si AA´es la bisectriz del ángulo A, donde A´es su pie sobre la hipotenusa de ABC, y si se verifica que, A´B = 2r, caracterizar el triángulo que verifica esta propiedad.

Romero, J. B. (2004): Propuesta personal

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante, de Córdoba (1 de abril de 2004).

De la condición dada en el enunciado se derivan los siguientes hechos de interés:

Sea A’B = 2r; siendo r el radio de la circunferencia inscrita en el triángulo ABC.

Por el teorema de la bisectriz, , de donde se determina el valor del radio    .
Por otra parte, el triángulo es rectángulo en A y así, r = p-a, donde 2p= a + b + c.

Igualando ambas expresiones del mismo valor, tenemos que:

.
Desarrollando esta igualdad, obtenemos:

2∙(b+c)∙(p-a)-a∙c=0;              2p(b+c)-2a(b+c)-ac=0;         (a+b+c)(b+c)-2a(b+c)-ac=0;

a(b+c)+(b+c)²-2a(b+c)-ac=0;           -a(b+c)+b²+c²+2bc-2ab-2ac =0;

-ab-ac+a²+2bc-2ab-2ac=0; a²-2ac+2bc-ab=0;

Examinamos esta última expresión:       a²-2ac+2bc-ab=0;

Si dividimos por a², nos quedará:    

O lo que es lo mismo:                    

De esta última igualdad deducimos que a = 2∙c, lo que significa que el ángulo C ha de ser igual a 30º.
Por tanto el triángulo rectángulo en cuestión es el que tiene por ángulos:
A=90º; B=30º y C=60º.

Veamos que se verifica el recíproco, es decir:

Todo triángulo rectángulo de este tipo A=90º; B=30º y C=60º verifica que si AA´es la bisectriz del ángulo A, donde A´es el pie sobre la hipotenusa de ABC, entonces A´B = 2r.

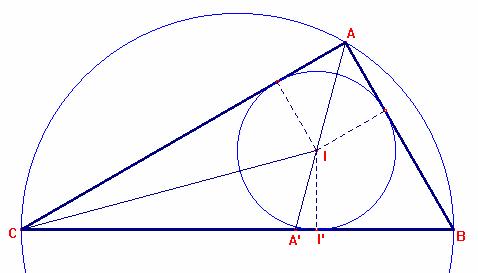
Con los datos considerados en la hipótesis de partida, A=90º; B=30º y C=60º deducimos las siguientes relaciones entre los lados de este triángulo:
a= 2.c; b= ;
Por tanto, si llamamos a x= A’B, por el teorema de la bisectriz tendremos que:

; de donde:

De la relación conocida entre las áreas del triángulos ABC; 2.p.r = b.c; deducimos que:          ;            

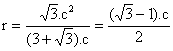
En definitiva, se tiene que, en efecto:

x =A’B = 2r,  c.q.d.