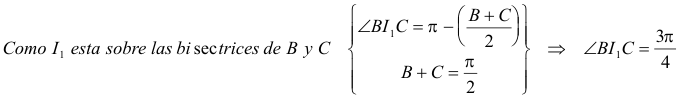Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid.

Problema 161:

Sea ABC un triángulo rectángulo en A, que tiene la siguiente propiedad :

Si AA’ es la bisectriz del ángulo A, donde A’ es su pie sobre la hipotenusa de ABC, y si se verifica que, A’B = 2r, caracterizar el triángulo que verifica esta propiedad.

Romero, J. B. (2004): Propuesta personal

Solución de José María Pedret. Ingeniero Naval. (Esplugas de Llobregat, Barcelona) (5 de abril de 2004)

UNA SOLUCION CABRI (Geometría dinámica)

Este es un problema que se puede resolver de forma elegante por medio del álgebra.

Si así lo hiciéramos, llegaríamos a la solución:

Esta relación es construible con regla y compás, con estos instrumentos hallaríamos la solución.

¿Qué ocurriría si no fuera construible con regla y compás y el álegbra llevara a ecuaciones intrabajables?

Ocurriría que deberíamos “jugar” con cabri para hallar la solución. Aunque no podríamos demostrar la exactitud de la solución en el sentido clásicamente aceptado, en el peor de los casos, podríamos hallar una configuración que nos conduciría a la resolución buscada.

APROVECHO ESTE PROBLEMA PARA ABORDAR UN METODO UTIL CON AYUDA DE CABRI.

(Lo cual no es muy descabellado, en una revista de triángulos y de CABRI)

Debo agradecer a François Rideau su inspiración al ver la ventaja que saca él “jugando” con CABRI.

También debo agradecer a Francisco Javier García Capitán su inspiración. El partido que, en ocasiones, saca del programa MATHEMATICA para llegar después a la solución geométrica, es verdaderamente admirable.

Yo quiero hacer algo parecido; pero usando CABRI.

Usamos la habilidad de CABRI II PLUS para manejar lugares geométricos en general.

1   Primero caracterizaremos el lugar geométrico de los incentros de un triángulo rectángulo cualquiera.

 El incentro está sobre la bisectriz ¿Cómo trazamos la bisectriz?

- Si ABC es rectángulo en A, entonces A está sobre el círculo de diámetro la hipotenusa (arco capaz de π/2).

- En cualquier triángulo, la bisectriz pasa por el punto medio del arco opuesto del triángulo circunscrito.

Por tanto, dado cualquier vértice A1 opuesto a la hipotenusa la recta A1M es la bisectriz.

A1' está en la intersección de la bisectriz y BC.

El incentro I1 está sobre el círculo de centro M que pasa por B y C (extremos de la hipotenusa). ¿Por qué?

este ángulo es suplementario de π/4, entonces I1 está en un círculo de ángulo capaz π/4 y cuerda BC; pero <OMC= π/2 que es el ángulo en el centro, pero el ángulo del arco capaz es mitad del ángulo en el centro y vale π/4 entonces I1 está sobre el círculo de centro M y que pasa por B y C.

I1 está en la intersección de la bisectriz y el círculo de centro M que pasa por B y C.

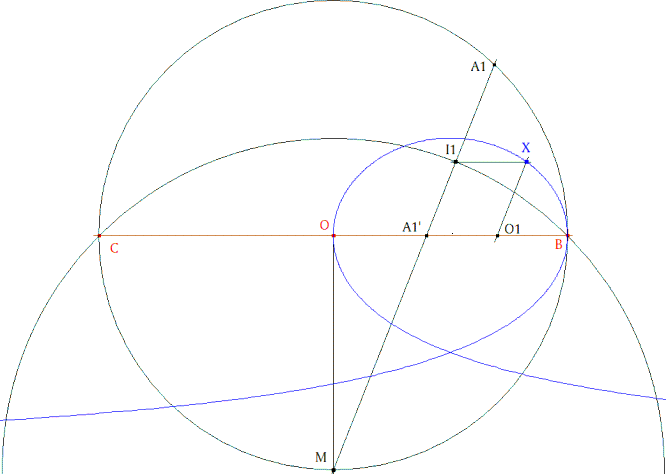
2   Primer lugar geométrico lugar geométrico

Trasladamos el radio O1A1' a I1.

Por O1, trazamos la paralela a la bisectriz que corta en X a la paralela a BC por I1.

Dibujamos el lugar geométrico de X cuando A1 se desplaza en su círculo.

Este es el lugar geométrico de los puntos sobre una paralela a BC que distan de I1 la mitad de A1B.

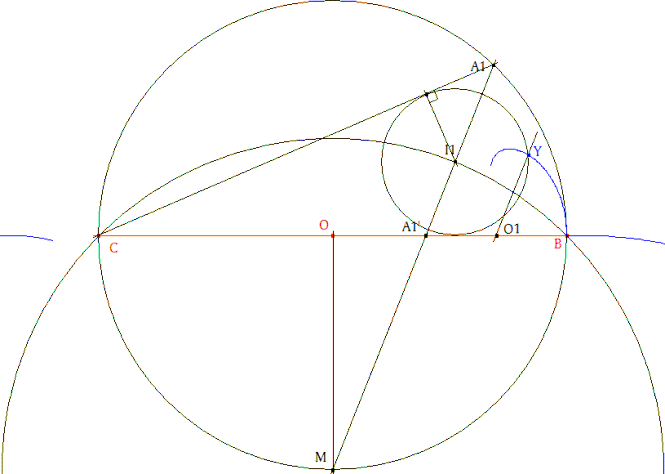
Segundo lugar geométrico.

Trazamos el círculo inscrito en el triángulo A1BC. De centro I1, pasa por el pie de la perpendicular de I1 a A1C.

El círculo circunscrito corta en Y a la paralela por O1 a la bisectriz A1M.

Dibujamos el lugar geométrico de Y cuando A1 se desplaza en su círculo.

Este es el lugar geométrico de los puntos de la paralela por O1 a la bisectriz y que pertenecen al círculo inscrito.

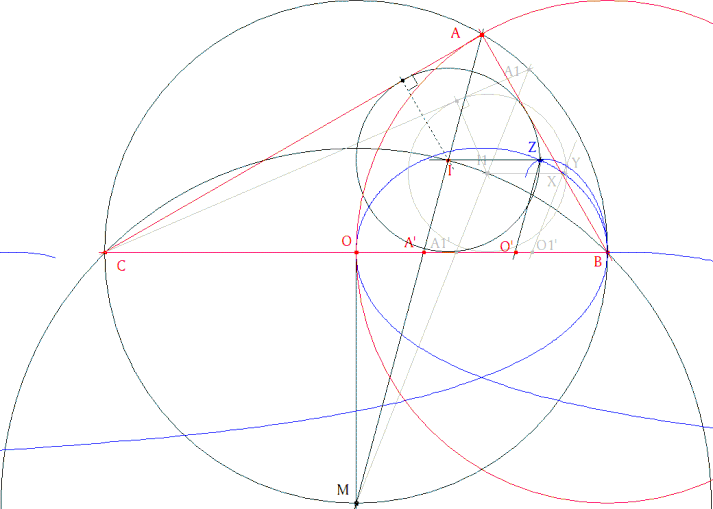
Si X e Y coinciden en un punto Z se cumple que el punto Z está sobre el círculo circunscrito y que el radio del círculo circunscrito es igual a la mitad de A’B. Por tanto Z está en el círculo solución.

Z es la intersección de los dos lugares geométricos.

- I está en la intersección de una paralela a BC por Z y el círculo de centro M que pasa por A y B.

- La bisectriz solución es la recta por I y por M.

- La intersección de IM con BC da A’.

- Y la intersección de IM con el círculo de diámetro BC nos da el vértice A.

Podemos dibujar el triángulo.

Si trazamos el círculo de centro B que pasa por O, vemos que A está sobre este círculo. BA es igual al radio del círculo de diámetro BC. Entonces el ángulo en B es de 60 grados.

Por lo tanto, es el triángulo rectángulo con ángulos agudos de