Problema 162

Sean ABC y A1 B1 C1 dos triángulos con los lados paralelos, uno en el interior del otro.

Si DEF es un triángulo circunscrito a uno e inscrito al otro, demostrar que:

(área DEF) (área DEF) = ( área ABC) (área A1 B1 C1)

Exercises de Géométrie, F.G.-M., pp.765-766, 6th Edition 1920, J. Gabay reprint, Paris, 1991

Solución  de Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz). (8 de abril de 2004)

Véase Fig.1

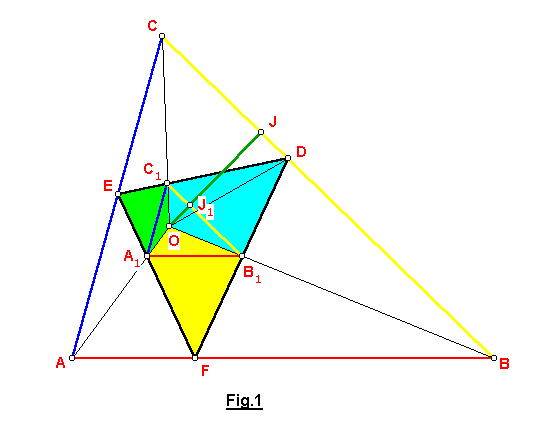
Como los lados de los triángulos ABC, A₁B₁ B₁ son paralelos, entonces AA₁, BB₁ y CC₁ son concurrentes en el punto O, ya que ambos triángulos son homotéticos.

Por la homotecia de centro O para los triángulos ABC y A₁B₁ B₁, tenemos:

Trazamos OJ ortogonal sobre BC, luego sabemos que:

También, J₁ es el punto de corte de OJ y B₁C₁, entonces:

 

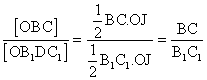
También:

 

 

Luego tenemos:

Además:

Por lo tanto, tenemos que:

 

Ahora:

[ABC] ² / [DEF] ² = 1/ k² ………. (I)

Por la homotecia:

[A₁B₁C₁] / [ABC] = k²……… (II)

A partir de (I) y (II):

             QED.