En todo triángulo, los puntos vecten V, V´ (exterior e interior) y el centro de la circunferencia de los nueve puntos F, están alineados.
DEMOSTRACIÓN MEDIANTE GEOMETRÍA ANALÍTICA. José Montes Valderrama. 26 de abril de 2004
Sea el triángulo ABC donde A está situado en el origen de coordenadas.
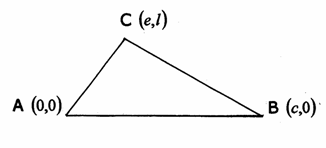 |
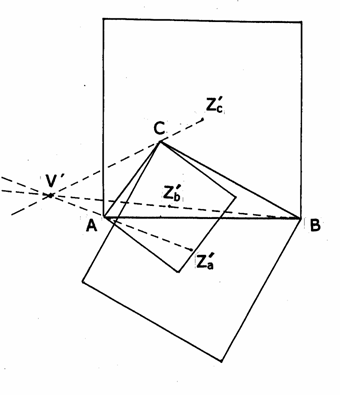
Para el cálculo de V y V´se necesitan en primer lugar los puntos de intersección de las diagonales de los cuadrados construidos sobre el exterior e interior respectivamente de los lados del triángulo:
Zc ![]() Z´c
Z´c ![]()
Za ![]() Z´a
Z´a
![]()
Zb ![]() Z´b
Z´b
![]()
CÁLCULO DEL PUNTO VECTEN EXTERIOR V
El punto V es la intersección de las tres rectas AZa, BZb, y CZb
 |
Del sistema formado por las rectas BZb, y CZc:
![]()
resulta el punto V 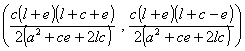
![]()
![]()
el cual pertenece a la tercera recta
AZa= ![]()
CÁLCULO DEL PUNTO VECTEN INTERIOR V´
El punto V´ es la intersección de las tres rectas AZ´a, BZ´b y CZ´c
 |
Del sistema formado por las rectas BZ´b, y CZ´c :
![]()
resulta el punto V´
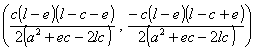
el cual pertenece a la recta AZ´a=
![]()
CENTRO DE LA CIRCUNFERENCIA DE LOS NUEVE PUNTOS
El centro de la circunferencia de los nueve puntos F está sobre la recta de Euler, en el punto medio de segmento determinado por el ortocentro O y el circuncentro H.
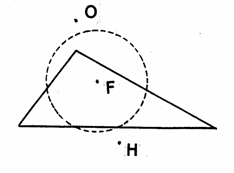 |
Teniendo en cuenta las coordenadas de O y H:
O 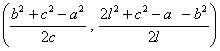 H
H
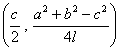
Se obtiene F como punto medio de los anteriores:
F 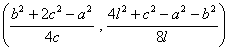
Sólo queda demostrar que V´,V y F están sobre una recta.
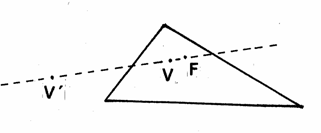 |
Para ello se tiene que verificar:
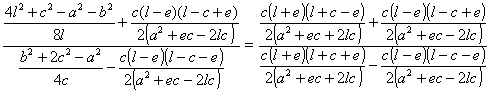 Þ
Þ
![]()
teniendo en cuenta que: ![]() y que
y que
![]() , entonces,
, entonces,
![]()
![]()
ambos denominadores son iguales a:
![]()
Ahora sólo queda demostrar la igualdad de los numeradores cuyos dos miembros son:
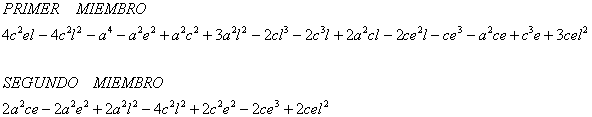
teniendo en cuenta que :
![]()
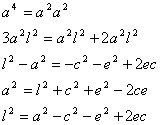
el primer miembro puede sufrir las siguientes transformaciones:
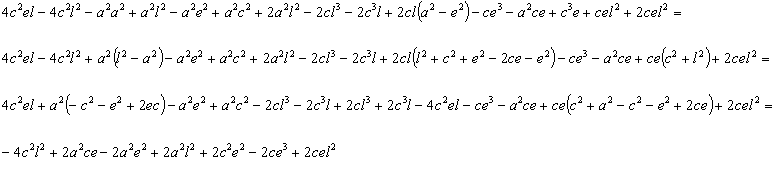
expresión última que coincide con el segundo miembro.