Propuesta de José Montes Valderrama, profesor del Centro Público de Adultos ·"Triana", Sevilla .
Problema 163.LEMOINE
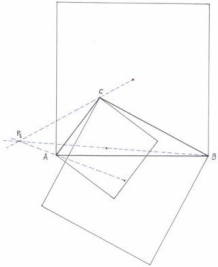
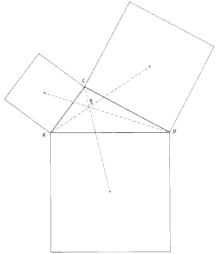
De forma análoga a como se obtienen los dos puntos de Fermat, construimos un cuadrado sobre cada uno de los lados de un triángulo y unimos cada centro de estos cuadrados con el vértice opuesto (del lado sobre el que está el cuadrado) del triángulo.
Así, se obtiene PI cuando los cuadrados se construyen por el interior de los lados del triángulo:
Este es el llamado INNER VECTEN POINT X(486) de la lista de Kimberling. Cuando los cuadrados se construyen por el lado exterior, se obtiene el punto PE: Este es el llamado VECTEN POINT X(485)
Pues bien PI , PE , y el centro de la circunferencia de los nueve puntos F siempre están alineados.
¡Y CON EL PUNTO K DE LEMOINE TAMBIEN!
Montes(2004): Propuesta personal.
El editor agradece a Darij Grinberg de Karlsruhe (Germany) que comunicara a Juan Carlos Salazar la ampliación de esta recta de Montes al punto de Lemoine.
Solución de la ampliación al punto de Lemoine de José María Pedret Ingeniero Naval. (Esplugas) (27 de abril de 2004)
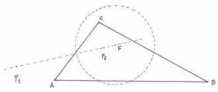
Como en el caso del punto F, para resolver este problema usaremos la vía algebraica y la trigonométrica.
Usaremos coordenadas baricéntricas y coordenadas trilineales.
Ver http://mathworld.wolfram.com/BarycentricCoordinates.html
Sabemos que:
Dados dos puntos P y R de coordenadas trilineales (p1, p2, p3) y (r1, r2, r3) y coordenadas baricéntricas (ap1,bp2,cp3) y (ar1,br2,cr3) respectivamente. La ecuación de los puntos T sobre la recta PR en coordenadas baricéntricas es:
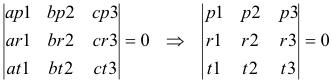
Ver http://faculty.evansville.edu/ck6/encyclopedia/
- Coordenadas trilineales de K: sin(A) : sin(B) : sin(C) PUNTO DE LEMOINE
- Coordenadas trilineales de PE: sec(A - pi/4) : sec(B - pi/4) : sec(C - pi/4)
- Coordenadas trilineales de PI: sec(A + pi/4) : sec(B + pi/4) : sec(C + pi/4)
Busquemos entonces el valor del siguiente determinante:
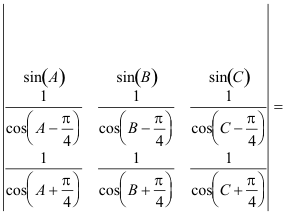
Recordando la resolución para el caso del punto F centro del círculo de nueve puntos nos quedaría
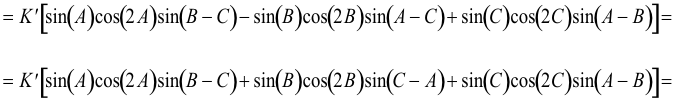
como
y como
![]()
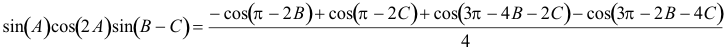
además
![]()
entonces
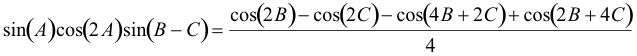
recordando de nuevo
![]()
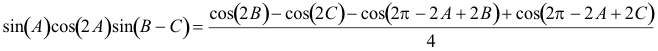
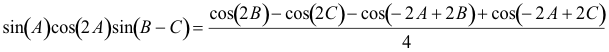
poniendo en columna los sumandos del determinante veremos como se cancelan los términos hasta anular el determinante
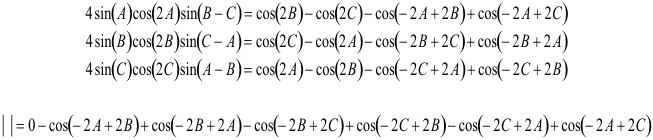
y para acabar
![]()
por lo tanto
![]()
Como el determinante es nulo PE, PI y el Punto de Lemoine están alineados. c.q.d