In memoriam. Miguel de Guzmán Ozámiz.
A un extraordinario matemático y geómetra
Quincena del 16 de abril de 2004 al 30 de abril de 2004
| Para el aula. Paroblema 164 Relaciones en un triángulo rectángulo: b=a sen B, c= a sen C. Relación entre los lados y ángulos de un triángulo oblicuángulo: a/sen A = b/sen B = c/ sen C Sánchez, E. (1901): Tablas de logaritmos, trigonométricas y de cálculos de intereses. Madrid. Pag LXVIII. Por Eusebio Sánchez Ramos, Catedrático de Matemáticas del Instituto de Logroño. Obra aprobada por la Real Academia de Ciencias. Comprende esta obra una tablas de logaritmos vulgares, con seis decimales... Cuarta edicion estereotipada de nuevo al galvanismo y considerablemente aumentada. Madrid Librería de Hernando y Compañía, calle del Arenal, núm 11. |
Solución de la alumna Maite Peña Alcaraz de 2º de Bachillerato del Colegio Portaceli de Sevilla
La primera parte se puede demostrar por el Teorema de Tales:
Si en la circunferencia goniométrica (de radio unidad), se cumple:
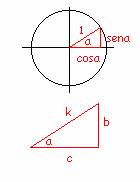
Luego 1/k=b/sena=c/cosa, luego b=ksena, y c=kcosa=ksen(90-a), y queda probado.
Para probar la segunda parte uso esta prueba, y utilizo una altura del triángulo dado:
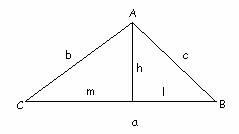
Y ahora sabemos que h=bsenC=csenB, y al operar, b/senB=c/senC. Usando otra altura se consigue la otra parte de la igualdad.