Problema 166
Sean el círculo circunscrito a un triángulo ABC y H el punto de encuentro de las alturas. Si se prolonga la altura CG hasta F se tendrá: GH = GF.
(Se precisa que G es el punto de corte de la altura desde C con el lado AB o su prolongación. F es el punto de corte de la altura con la circunferencia circunscrita.)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

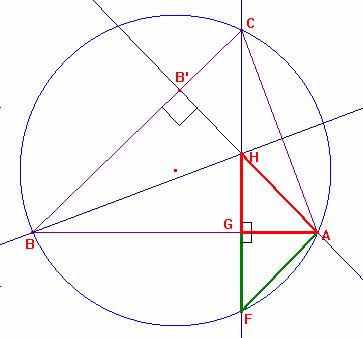
            Examinamos los dos triángulos rectángulos semejantes AB’B y AGH. Para nuestro interés, tenemos que el ángulo <B es igual al ángulo <H. Como quiera que el ángulo <B y el ángulo <F están inscritos en la misma circunferencia y subtienden ambos la misma cuerda AC, dichos ángulos serán iguales,  <F = <H.
            Así ya los dos triángulos rectángulos AGH (rojo) y AGF (verde) tienen los tres ángulos iguales y uno de los catetos es común a ambos, entonces de esta manera deberán coincidir los otros elementos. En particular, GH = GF, c.q.d.