Problema 166.- Solución de Ricard Peiró i Estruch, profesor de Matemáticas del IES 1 de Xest (València) (2/ 5 / 2004)
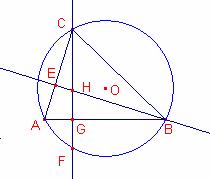
En cualquier 
consideramos
la altura al vértice C y el pie de la altura G.
Sea H el ortocentro del triángulo.
La altura al vértice C
corta la circunferencia circunscrita del triángulo en el punto F. Entonces:
.
Demostración:
Consideramos la circunferencia
circunscrita del triángulo .
Podemos notar que
por ser
ángulos sobre rectas perpendiculares.
por
ser ángulos inscritos que abarcan el mismo arco.
Entonces los triángulos
son iguales
porque son rectángulos, tienen un ángulo agudo igual y un cateto 
igual.
Entonces, .
Prueba con Cabri: