Problema 166

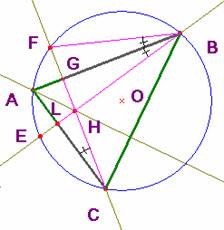
126.- Sean el círculo circunscrito a un triángulo ABC y H el punto de encuentro de las alturas. Si se prolonga la altura CG hasta F se tendrá: HG =GF.(Traducción literal del editor. Se precisa que G es el punto de corte de la altura desde C con el lado AB o su prolongación. F es el punto de corte de la altura con la circunferencia circunscrita. )

André, M. Ph. (1920). Éléments de GÉOMÉTRIE Conformes aux programmes de baccalauréats (1re partie) de l'enseignement secondaire classique et de l'enseignement secondaire moderne. Contenant plus de mille problémés résolus et a resoudre.(Treinte-quatriéme edition). Paris, Librairie classique de FE André Guédon.E. Andre Fils Succeseur, 6 rue Casimir-Delavigne (près l'Odeon). (p. 83)

Solución Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca)

Los triángulos HLC y HGB son semejantes, pues son rectángulos y tienen igual el ángulo en H; por consiguiente son iguales los ángulos <GBH y <HCL y este último igual a <FCA y a <FBA por abarcar el mismo arco. En consecuencia, AB es una bisectriz del triángulo FBH y también su altura, y por ello, es su mediatriz y su mediana, luego FG = GH como se pretendía demostrar.