Propuesto por el profesor Saturnino Campo Ruiz, del IES Fray Luis de León de Salamanca

Problema 167

77.- Se da el triángulo ABC. Se trazan cevianas cualesquiera AA', BB' y CC' que concurren en D. Se quiere que el triángulo homológico sea equilátero y que el punto homólogo del D sea el ortocentro.

Olabarrieta L. (S.J.)(1945) : Geometría y Trigonometría. Bilbao. (p 449)

El profesor Saturnino Campo propone esta nueva redacción para el problema

Sea ABC un triángulo y D un punto del plano no situado en ningún lado (ni en sus prolongaciones). Probar que existe alguna homología que transforma el triángulo ABC en un triángulo equilátero y el punto D en el centro de ese triángulo. Si se elige un punto A* como homólogo del vértice A, la homología es única. Determinarla .

Solución de José María Pedret, Ingeniero Naval, Esplugues de Llobregat (Barcelona)

En el problema 137 de la página de RICARDO BARROSO CAMPOS, preparamos un estudio para los métodos para encontrar las intersecciones de rectas con cónicas dadas por puntos ( y/o tangentes) y el trazado de tangentes a dichas cónicas.

sol/sol137pedcp.pdf

La recta proyectiva es un espacio proyectivo de dimensión n=1 y una referencia proyectiva de la recta está constituida por n+2=3 puntos.

El plano es un espacio proyectivo de dimensión n=2; por tanto, una referencia proyectiva del plano está constituida por cuatro puntos tres a tres no alineados.

Atendiendo al enunciado del profesor Saturnino Campos podemos decir que A, B, C y D constituyen una referencia del plano.

Antes de seguir, veamos que es una homografía y en particular una homología.

HOMOGRAFIA (1)

Sea ^h :E→E' un isomorfismo de espacios vectoriales, como transforma rectas vectoriales en rectas vectoriales, induce una biyección h: P(E)→P(E') que recibe el nombre de homografía de P(E) en P(E'). Si X es un punto, escribiremos h(X) o X'.

Una homografía conserva puntos alineados (rectas en rectas) y conserva la razón doble.

En particular, para este problema, nos interesa explicitar más la definición como lo hace Pedro Puig Adam en su Geometría Métrica Tomo II.

HOMOGRAFIA (2)

Dos figuras planas son homográficas cuando se corresponden punto a punto y recta a recta, de tal modo que a todo punto y recta incidentes en una de las figuras correspondan un punto y una recta también incidentes en la otra.

Para definir una homografía, necesitamos la imagen de los componentes de una referencia proyectiva del plano . En este caso cuatro puntos.

Atendiendo al enunciado las imágenes de A, B, C y D nos definen la homografía. De momento, podemos afirmar que existe una homografía que transformará A, B, C y D en los vértices y centro del triángulo equilátero del enunciado.

Pero el enunciado nos pide que las figuras sean homológicas. Veamos la definición de homología.

HOMOLOGIA (1)

Se llama homología a una homografía de un plano proyectivo distinta de la identidad y que posee una recta de puntos fijos. Esta recta se denomina EJE DE HOMOLOGIA.

TEOREMA

Una homografía h: X→X' es una homología si y sólo si existe un punto O tal que, para todo punto distinto de O, la recta XX’ pasa por O. Este punto se denomina CENTRO DE HOMOLOGIA.

También aquí, nos interesa explicitar más la definición como Pedro Puig Adam en su Geometría Métrica Tomo II o Michel Chasles en su Traité de Géométrie Supérieure.

HOMOLOGIA (2).

- Los puntos homólogos están alineados con un punto fijo O (CENTRO DE HOMOLOGIA).

- Las rectas homólogas se cortan en una recta fija (EJE DE HOMOLOGIA).

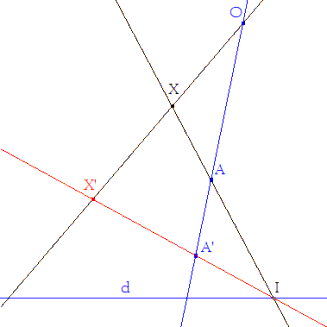
 CONSTRUCCION GEOMETRICA DE LA IMAGEN DEL PUNTO POR LA HOMOLOGIA.

De acuerdo con lo anterior, consideremos una homología h de eje d y centro O. Elijamos un punto A distinto del centro O y que no pertenece al eje. Si X es distinto de O y no pertenece a d, podemos construir su imagen h(X) = X’ del modo que sigue:

figura 1  

- Si X no pertenece a AA’, se traza la recta AM que corta al eje d en un punto I. El punto X’ está en la intersección de las rectas IA’ y OX (figura 1).

figura 2  

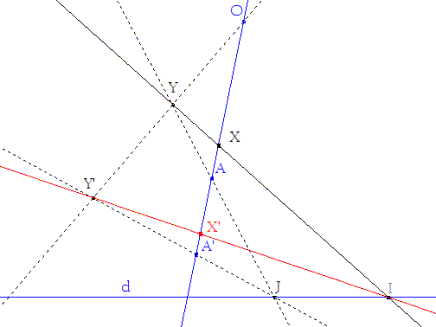
- Si X pertenece a la recta AA’, volvemos al caso anterior eligiendo un punto auxiliar Y no situado en AA’ (figura 2).

PUNTOS DEL INFINITO

Aquí sólo recordaremos lo justo para utilizarlo en nuestro problema, aprovechando la intuición que tuvo Desargues cuando “intuyó” a la recta proyectiva como una recta afin más un punto del infinito o al plano proyectivo como un plano afin más la recta del infinito.

Multitud de libros de Geometría Proyectiva dan una base sólida y rigurosa de lo anterior. Yo consultaría a Jean-Claude Sidler en su Géométrie projective. Cours, exercices et problèmes corrigès, Dunod. París; porque el lenguaje es suficientemente moderno y riguroso y además su tono “no empalagosamente bourbakiano” lo hace muy comprensible y fácil de trasladar a los problemas clásicos que en muchos casos nos ocupan.

Para este problema, precisamente usaremos unas propiedades de los puntos del infinito tal com lo hace Michel Chasles en su Traité de Géométrie Supérieure.

RECTA LIMITE

A los puntos de una figura situados en el infinito corresponden, en la figura homográficas, puntos situados en línea recta. La recta imagen del infinito de cada una de las figurad recibe el nombre de RECTA LIMITE.

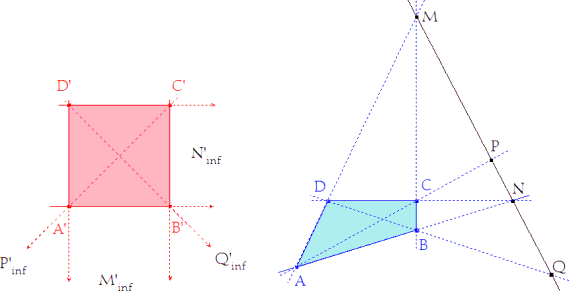
Sea r_∞ la recta del infinito de la figura origen y sea r’_∞ la recta del infinito de la imagen.

Es costumbre escribir h(r_∞)=j’ y h(i)=r’_∞. Las rectas límite se notan respectivamente i, j’.

EJEMPLO PREVIO (figura 3)

Para precisar el manejo del infinito en el plano, Chasles nos hace ver que todo punto de la recta i tiene su homólogo en el infinito de la figura imagen y así, a dos rectas paralelas de la imagen corresponden en la figura de partida dos rectas concurrentes en un punto de i. Fijaremos ideas observando al cuadrado A’B’C’D’ como imagen del cuadrilátero ABCD.

figura 3  

M=BC ∩ DA y N=AB ∩ CD; M y N son las imágenes de los puntos del infinito M’ y N’. La recta MN es la recta límite del cuadrilátero ABCD. Podemos ahora establecer que:

El punto en el infinito sobre j’ (la recta límite de la imagen) es la imagen del punto en el infinito de i (recta límite de la figura original).

Establecido lo anterior, podemos decir que una recta paralela a la recta i en la figura original le corresponde una recta paralela a j’ en la imagen.

Con todo lo visto hasta aquí podemos atacar la demostración que pide el enunciado del problema y luego la construcción de la solución pedida. Para la demostración, echamos mano del siguiente

TEOREMA

Dadas dos figuras homográficas, si tres rectas de la primera figura concurren en un punto C y además coinciden con sus respectivas rectas homólogas, entonces lo mismo ocurrirá para todas las rectas que pasen por dicho punto C. (Ver la obra citada de Chasles)

TEOREMA

DOS FIGURAS HOMOGRAFICAS EN GENERAL (sin un sistema de dos rectas homologas coincidentes en el infinito) SIEMPRE PUEDEN COLOCARSE DE MANERA QUE LAS FIGURAS SEAN HOMOLOGICAS

DEMOSTRACION

Paso I

Hallemos las rectas límite i y j’ y supongamos que tales rectas son paralelas.

Paso II

Sea un punto E∈i ⇒ h(E) = E’ = ∞’; entonces todas las recta que pasan por E tienen sus homólogas paralelas entre sí (diríamos que se cortan en ∞’), y podemos determinar su dirección. Trazamos por E una recta e paralela a esa dirección y sea h(e)=e’ su imagen; las rectas e y e’ son entonces paralelas entre sí.

Hagamos la misma operación con otro punto F∈i y obtenemos las rectas paralelas f y f’.

Paso III

Sea el punto S=e ∩ f y S’=e’ ∩ f’. Podemos colocar la figura imagen haciendo coincidir S con S’, e con e’ y f con f’.

ENTONCES LAS FIGURAS SON HOMOLOGICAS Y SU CENTRO DE HOMOLOGIA ES S.

Conclusión IV

En efecto, la recta de la primera figura por S y paralela a i y a j’ es su propia homóloga, por que tiene dos puntos homólogos coincidentes en S y además el punto en del infinito de esa recta coincide también con dos puntos homólogos. Pero e y f también concurren en S con esa recta y coinciden también con sus homólogas e’ y f’, entonces aplicando el teorema anterior, las dos figuras son homológicas.

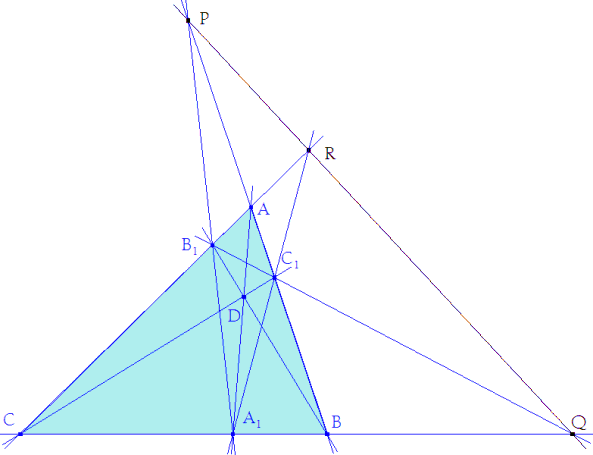
Nota

El enunciado de Olabarrieta es desafortunado en la notación, aquí emplearemos A’, B’ y C’ para los puntos homólogos y A₁, B₁ y C₁ para los puntos de intersección de las cevianas con los lados del triángulo.

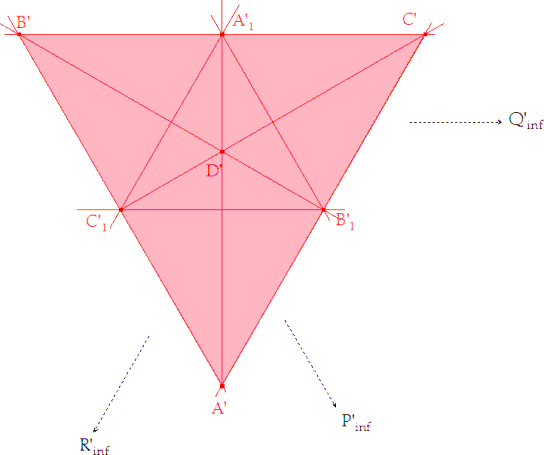
PUNTOS DEL INFINITO EN EL TRIANGULO EQUILATERO (figura 4)

Con todo lo visto, estamos en condiciones de resolver el problema; pero antes y estudiaremos como se comportan los puntos del infinito cuando la homología debe ser entre dos triángulos y uno de ellos equilátero.

figura 4  

Para establecer los puntos del infinito en el triángulo equilátero, determinamos las direcciones de las rectas paralelas cuyas homólogas se conocen en el triángulo de partida. Así escribiremos:

P’_∞= A’B’ ∩ A₁'B₁', Q’_∞= B’C’ ∩ B₁'C₁', R’_∞= C’A’ ∩ C₁'A₁',

Este análisis de la figura del triángulo equilátero nos permite determinar la recta límite i en el triángulo que dice el enunciado.

FIJEMONOS ADEMAS QUE HEMOS ESTABLECIDO LOS PUNTOS DEL INFINITO OBLIGANDO A LAS CEVIANAS A PASAR POR EL CENTRO D’, LO CUAL IMPLICA QUE UNA VEZ CONSTRUIDA LA HOMOLOGIA LA IMAGEN DEL PUNTO D SERA D’, COMO PIDE EL ENUNCIADO (y ya se intuye en la próxima figura).

RECTA LIMITE EN UN TRIANGULO CUALQUIERA (figura 5)

figura 5  

Hemos visto, en la figura anterior que los puntos del infinito del triángulo equilátero viene dados por:

P’_∞= A’B’ ∩ A₁'B₁', Q’_∞= B’C’ ∩ B₁'C₁', R’_∞= C’A’ ∩ C₁'A₁',

Basta observar la figura para comprender que la recta PRQ es i, la recta límite buscada ya que:

P = AB ∩ A₁B₁, Q = BC ∩ B₁C₁, R = CA ∩ C₁A₁, Y HEMOS OBLIGADO A LAS CEVIANAS A CONCURRIR EN D.

Ya sólo nos falta trazar las rectas que nos permitan determinar el centro de homología O.

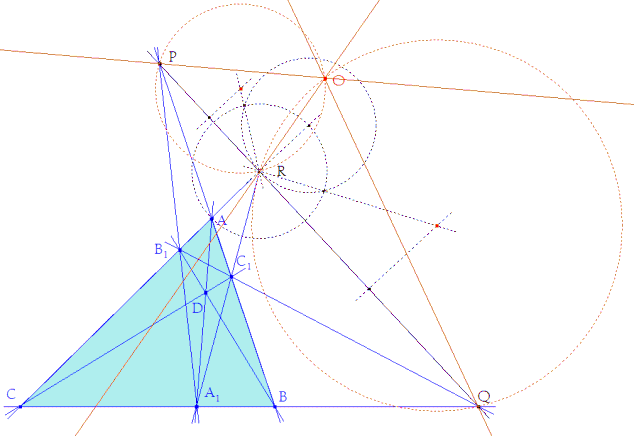
DETERMINACION DEL CENTRO DE HOMOLOGIA BUSCADO (figura 6)

Para la demostración del enunciado, tomamos dos puntos sobre la recta i, y trazamos por ellos sendas rectas. Estas rectas son son paralelas a sus homólogas. Luego, con su intersección, determinamos el centro de homotecia O y podemos colocar las figuras coincidiendo el centro hallado y las dos rectas.

Nosotros conocemos bien los puntos de la recta límite pues P, Q y R pues deben ser homólogos a los puntos del infinito del triángulo equilátero P’_∞, Q’_∞ y R’_∞.

Las direcciones que definen estos puntos forman entre sí ángulos de π/3 (figura 4).

a La dirección de Q’_∞ forma un ángulo de π/3 con la dirección de R’_∞ y por lo tanto las dos rectas por formarán un ángulo cuyo vértice /punto de intersección) estará sobre el arco capaz de π/3 y cuerda QR, luego el centro de homología estará sobre este arco capaz.

b La dirección de R’_∞ forma un ángulo de π/3 con la dirección de P’_∞ y por lo tanto las dos rectas por formarán un ángulo cuyo vértice estará sobre el arco capaz de π/3 y cuerda RP, luego el centro de homología estará sobre este arco capaz.

Veamos la construcción en la figura 6

figura 6  

El centro de homografía O estará en la intersección de los dos arcos capaces y cualquier recta paralela a la recta límite puede ser eje de homografía. Construyamos la homología pedida; pero antes coloquemos el triángulo equilátero en posición.

LOS ARCOS CAPACES QUE PODEMOS TRAZAR AL OTRO LADO DE LA RECTA LÍMITE NOS DARÍAN UNA SEGUNDA SOLUCIÓN PARA EL CENTRO DE HOMOLOGÍA.

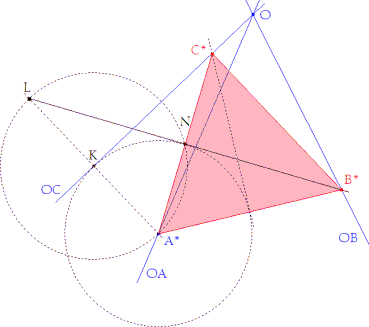
COLOCAR EL TRIANGULO EQUILATERO (figura 7)

Dadas tres rectas OA, OB y OC, colocar el triángulo equilátero, equivale al siguiente problema: Inscribir un triángulo semejante a otro dado con los vértices en cada una de tres rectas dadas.

Problema conocido por los”fans” de RICARDO BARROSO, resuelto de forma general en el nº 99

sol/sol99ped.htm

El caso del triángulo equilátero presenta una serie de simplificaciones que vale la pena mostrar

figura 7  

- Dado el punto O y las rectas OA, OB y OC, tomamos un punto A* sobre la recta OA.

- OC es cortado por una perpendicular desde A* en el punto K.

- Círculo por A* con centro en K y círculo por K con centro en A* que corta a KA* en L.

- Los círculos se cortan en N.

- LA*=2KA*=2NA*, como ∠LNA*=π/2, entonces ∠LA*N=π/3.

- LN es la imagen por rotación de centro A* y ángulo π/3 de la recta OC.

- B* está en la intersección de LN con OB

- Ahorramos la siguiente rotación, no necesaria, pues la mediatriz de A* y B* corta a OC en C*.

En una primera construcción de la solución, usaba este método; pero una comunicación de SATURNINO CAMPOS, que me ha llegado a través de RICARDO BARROSO, me ha hecho ver que es mucho más elegante y acorde con la construcción de la homología el hacer la construcción siguiendo los pasos de la demostración, en especial el

 Paso II:

... entonces todas las recta que pasan por E tienen sus homólogas paralelas entre sí (diríamos que se cortan en ∞’), y podemos determinar su dirección...

EL TRIÁNGULO EQUILATERO HOMOLOGO

figura 8

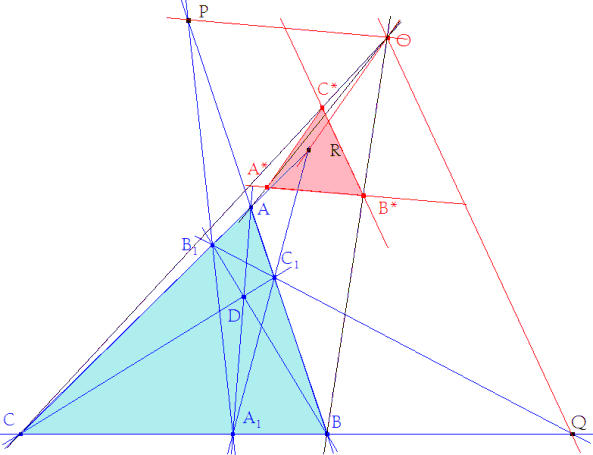
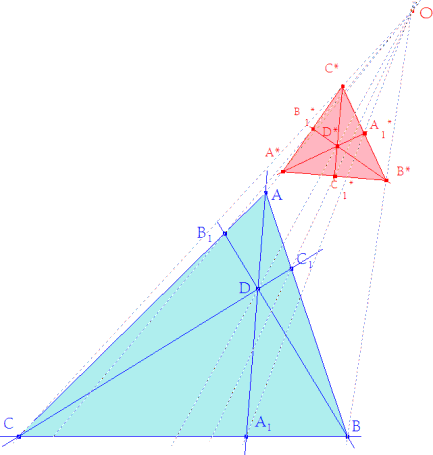
- Hallado O, construimos OA, OB y OC. Tomamos A* sobre OA.

- P= AB ∩ A₁B₁, entonces la dirección A*B* es paralela a OP.

    Por A* una paralela a OP que corta a OB en B*.

- Q= BC ∩ B₁C₁, entonces la dirección B*C* es paralela a OQ.

    Por B* una paralela a OQ que corta a OC en C*.

Y comprobamos que

- R= CA ∩ C₁A₁, entonces la dirección C*A* es paralela a OR.

    Por C* una paralela a OR corta a OA en A*.

Y ahora como la homología es una homografía (a todo punto y recta incidentes en una de las figuras correspondan un punto y una recta también incidentes en la imagen) y como hemos impuesto que el punto D tenga su homólogo en el centro del triángulo equilátero podemos afirmar que:

la imagen de A₁ es A₁*, punto medio de B*C*, A₁= AD ∩ BC, entonces A₁*= A*D* ∩ B₁*C₁*;

la imagen de B₁ es B₁*, punto medio de C*A*, B₁ = BD ∩ CA, entonces B₁*= B*D* ∩ C₁*A₁*;

la imagen de C₁ es C₁*, punto medio de B*C*, C₁ = CD ∩ AB, entonces C₁*= C*D* ∩ A₁*B₁*;

TODOS LOS PUNTOS HOMOLOGOS (figura 9)

Presentamos la figura con los puntos homólogos, ocultando las líneas auxiliares para mayor claridad.

figura 9  

UN POCO MAS

En el curso de Geometría Métrica de Pedro Puig Adam, en su Tomo II de complementos podemos encontrar el siguiente enunciado en el ejercicio 27 del capítulo VI:

Colocar un cuadrilátero dado ABCD (de lados no paralelos) y un cuadrado dado A’B’C’D’ en posición tal que sean homológicos

Este ha sido la base del desarrollo que he seguido. La diferencia principal en este problema es que las direcciones a determinar deben ser perpendiculares (como los lados del cuadrado) y por lo tanto los arcos capaces serán las semicircunferencias de diámetros QR y PR.

Aunque sean algo mas farragosas y con el estilo más antiguo, leer a Michel Chasles en su Traité de Géométrie Supérieure ha sido clarificador y muy provechoso para hilvanar la demostracion. Chasles publicó su libro en 1852.

Tal vez podría rescribirse este problema en un lenguaje y notación actuales; pero lo que he pretendido, en todo momento, es que lo explicado se traduzca rápidamente en algo construible con regla y compás.

Gracias a Ricardo Barroso por su página. Si alguien me obligara a resolver los problemas casi seguro que no lo haría. La afición y entusiasmo que él genera es la principal gasolina.