Problema 167

77.- Se da el triángulo ABC. Se trazan cevianas cualesquiera AA', BB' y CC' que concurren en D. Se quiere que el triángulo homológico sea equilátero y que el punto homólogo del D sea el ortocentro.

Antes de pasar a resolver el problema necesitamos precisar unos conceptos y resultados que serán usados posteriormente.

1.- Homologías. Generalidades.

Una homología del plano proyectivo es una transformación puntual del plano en sí mismo tal que las rectas que unen los pares de puntos homólogos son concurrentes en un punto O llamado centro de la homología, y de otra parte las rectas homólogas se cortan en puntos de una misma recta e que llamamos eje de la homología.

Si una recta pasa por el centro de homología se transforma en ella misma: es invariante (no fija) por la homología.

2.-Rectas límite de una homología. Homólogo de un punto.

Son aquellas rectas homólogas de la recta del infinito del plano. Precisando: la recta límite l, es aquella que se transforma en la recta del infinito. La recta límite k’ es la imagen de la recta del infinito. Son la antiimagen (recta l) y la imagen (recta k’) de la recta del infinito en la homología de centro O y eje e.

Las rectas límite son paralelas al eje de homología, pues han de concurrir con él en la recta del infinito o recta impropia.

Según la definición una homología queda determinada conociendo el centro, el eje y un par de puntos homólogos. Para construir B’, imagen de B, trazamos la recta r determinada por A y B, que corta al eje en un punto Q y la recta OB que ha de contener a B’. La recta homóloga de r, r’ también corta al eje en Q, y por consiguiente, el punto B’ se obtiene de la intersección de las rectas A’Q y OB.

Una homología también queda determinada si se conocen el centro, una recta límite, por ejemplo l y un par de puntos homólogos. Intentaremos primeramente determinar el eje de homología y entonces podremos referirnos al caso anterior.

3.- Construcción de las rectas límite.

De la definición dada de las rectas límite, se deduce que si dos rectas se cortan en un punto de la recta límite l, sus imágenes por la homología son dos rectas paralelas. Veamos cómo pueden determinarse las rectas límite de una homología donde se conocen el centro, el eje y un par de puntos homólogos.

Para construir l bastará con encontrar un punto L de una recta dada r, cuya imagen sea un punto impropio L’ de la recta homóloga r’. Cualquier recta paralela a r’ la cortará en el punto impropio L’. Esto es, L es la intersección de r* con r. Trazando una paralela al eje por L queda determinada la recta límite l.

Análogamente se procedería para construir la otra recta límite k’.

Vemos pues que si una recta m corta a la recta límite l en un punto L_m, como la imagen de éste, está en el infinito, (es el punto impropio de la recta m’), y la recta determinada por el centro O y el punto L_m se transforma en sí misma ha de suceder que las rectas m’ y OL_m son paralelas, y, por tanto, para dos rectas cualesquiera, m y n se tiene esta importante propiedad para la resolución del problema:

Los ángulos que forman las transformadas m’ y n’ de las rectas m y n son iguales o suplementarios a los ángulos determinados por las rectas OL_m y OL_n.

4.- La polar de un punto respecto de un triángulo.

Si las rectas AA’, BB’ y CC’ son concurrentes en D, las rectas A’B’, BB’ y CC’ cortan a los lados opuestos en puntos de la misma recta P, Q y R., llamada polar de D respecto al triángulo ABC.

Demostración.

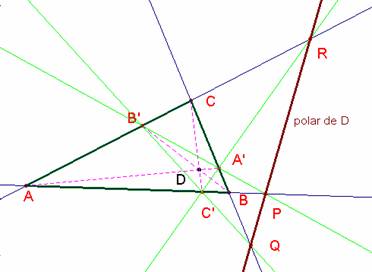
La recta A’B’, corta al lado AB en P, que según se vio en el problema nº 151, por aplicación de los teoremas de Menelao (en el triángulo ABC cortado por la transversal B’A’) y Ceva (para las cevianas concurrentes en D) es tal que (ABC’P)= —1, de donde se sigue (C’AB) = — (PAB). Con las otras rectas ocurre igual y se tienen (A’BC)= —(QBC) y (B’CA)= —(RCA). El producto de estas relaciones (PAB)·(QBC)· (RCA) = —(C’AB)· (A’BC)· (B’CA)= —(—1) = +1 demuestra la alineación de los P, Q y R..

(La notación (JKL) representa la razón simple de estos puntos, es decir, (JKL) =)

La recta determinada a partir del triángulo y el punto D se denomina polar del punto respecto al triángulo.

5.- Resolución del problema.

Si existe la homología buscada que transforme ABC en el triángulo equilátero A*B*C*, también transformará las cevianas MM’ en los correspondientes segmentos del triángulo equilátero paralelos a cada base. Por consiguiente las rectas AB, A’B’; AC, A’C’ y BC, B’C’ al transformarse por la homología en rectas paralelas, han de ser concurrentes dos a dos, en puntos de la recta límite l. Definimos pues los puntos. L_a , L_b y L_c como las intersecciones de los pares de rectas MN y M’N’.

Que estos tres puntos están alineados es lo que acabamos de demostrar, la recta límite l de la homología que buscamos es la que hemos llamado anteriormente, la recta polar del punto D con respecto al triángulo ABC.

Para completar la homología nos hace falta determinar el centro y fijar la posición del homólogo de un vértice cualquiera del triángulo dado.

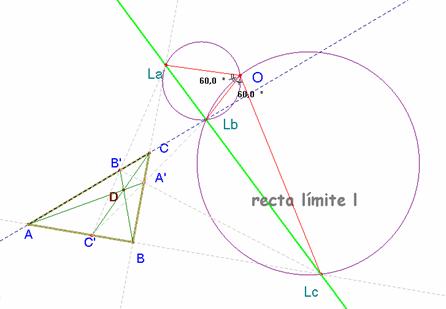
Llamando a, b y c a las rectas soporte de los vértices del triángulo ABC, sus transformadas por la homología a’, b’ y c’ forman un triángulo equilátero, según la conclusión final de 3 , el centro de homología O es un punto tal que las rectas OL_a , OL_b y OL_c forman entre sí ángulos de 60º o de 120º. El punto O, centro de homología, se hallará construyendo el arco capaz de los segmentos L_a L_b y L_b L_c y amplitud 60º.

Una homología también queda determinada conociendo el centro, una recta límite y el homólogo de un punto.

5.1.-Determinación del eje de homología.

Veamos, con estos datos, cómo se puede determinar el eje de la homología. Solamente necesitamos hallar un punto, pues sabemos que es paralelo a la recta límite. Supongamos que hemos dado el homólogo del punto A que voy a llamar A*.

Una recta que pase por A, por ejemplo la recta c (determinada por A y B), corta a la recta límite l en el punto L_c., cuya imagen por la homología es el punto impropio de la recta c’; por tanto esta recta c’ ha de ser paralela a la recta determinada por O y L_c (en el dibujo, el par de rectas de color cyan). Dos rectas homólogas se cortan en un punto del eje. Así se determina el punto R_c y con él, el eje de la homología.

La determinación de los homólogos de los restantes vértices y del punto D se hace como se ha explicado en 2, y, con un poco de paciencia se termina la construcción. Para calcular B*, tomo la recta AB, que pasa por B y corta al eje en el punto R_c. Su homóloga también pasa por este punto y es paralela a OL_c (las c y c’de antes). Como B* ha de estar sobre OB, el corte de éstas nos da el punto B*.

Para hallar C* tomo la recta BC. Su homóloga pasa por su corte con el eje, el punto R_a, y por B*. El punto C* es el que esta última recta tiene en común con OC.

D* se halla a partir de la recta CD que corta a la recta límite y al eje en los puntos L_d y R_d respectivamente. Su homóloga pasa por R_d y es paralela a la recta O L_d y su corte con OD proporciona el punto D*.