El circuncentro de un cuadrilátero cíclico es ortocentro de su triángulo auto polar

Teorema:

Sea ABCD un cuadrilátero inscrito en un círculo O. El punto de corte de sus diagonales AC y BD es P, las prolongaciones de AB, DC y CB, DA se cortan en Q y S respectivamente. Probar que: O es el ortocentro del triángulo PQS¹.

Demostración: Ver Fig.1

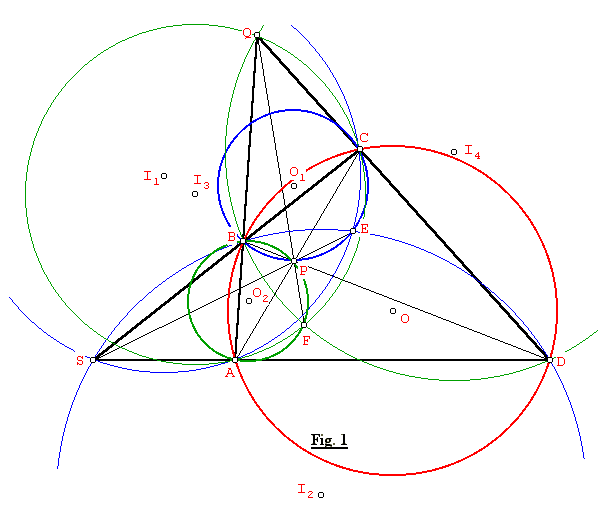
Trazamos los círculos circunscritos I₁ e I₂ de los triángulos SAC y SBD respectivamente, donde E es el otro punto de corte de I₁ con I₂, así tenemos que P es el centro radical de O, I₁ e I₂, luego S, P y E son colineales, también trazamos los círculos circunscritos I₃ e I₄ de los triángulos QAC y QBD respectivamente, donde F es el otro punto de corte de I₃ con I₄, de la misma manera P también es centro radical de O, I₃ e I₄, luego Q, P y F son colineales. También: <SCA = <SDB = < SEB entonces BPEC es un cuadrilátero cíclico y < QDB = <QAC = <QFB también BAFP es un cuadrilátero cíclico, entonces: SA.SD = SB.SC = SP.SE y QB.QA = QC.QD = QP.QF. Por lo tanto, los cuadriláteros CPFD y ADEP son inscriptibles con círculos circunscritos O₅ y O₇ respectivamente.

¹Este teorema aparece sin demostración en libro “Introducción a la Geometría Moderna” por Levi Shively PhD, pag. 112, CECSA, 1972.

Además, ver Fig.2, las prolongaciones de PE y PF cortan a CD y AD en H y G respectivamente, luego: <CEH = <PBC = <DBC = <DAC, además <HED = <CAD, entonces <CED = <CEH + <HED = 2 <CAD. Por otro lado: <AFG = <ABP = <ABD = <ACD, también <GFD = <PCD = <ACD, luego <AFD = <AFG + <GFD = 2<ACD.

Trazamos los circuncírculos O₃ y O₄ de los triángulos AFD y CED respectivamente cuyo punto de corte es O’, luego aplicando un conocido teorema: EPFO’ es un cuadrilátero cíclico con circuncírculo O₆. Debido a que tenemos cuatro círculos O₁, O₂, O₃ y O₄ con cuerdas BC, AB, AD y CD. En seguida, probaremos que O’ coincide con O.

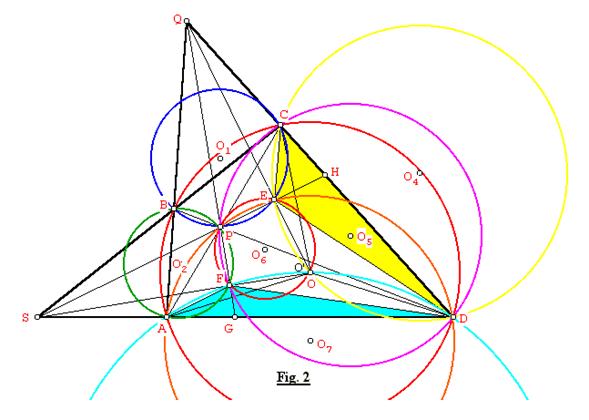
En el cuadrilátero inscrito AFO’D tenemos: <AFD = <AO’D = 2<ACD, también en el cuadrilátero inscrito CEO’D tenemos: <CED = <CO’D = 2<CAD. Luego con respecto al triángulo ACD, O’ es el cincuncentro, por lo tanto O’ coincide con O.

También, ver Fig. 3, las prolongaciones de CE y AF cortan a BD en J y K respectivamente, entonces: <JEP = <PBC = < DBC = <CAD y <JEO = <CDO = 90º- <CAD, además < PEO = <JEP + <JEO = 90º, similarmente: < PFO = <PFK + <KFO = 90º. Además en el cuadrilátero cíclico AFPB: <BFP = <BAP = <BAC y en el cuadrilátero cíclico ABCD: <BAC = <BDC. Ahora: <BFO = <PFO + <BPF = 90º + <BFP y <BCO = 90º - <BDC, entonces: <BFO + < BCO = 180º, por lo tanto BFOC es un cuadrilátero cíclico con circuncírculo O₈ sin dibujar, además S está sobre el eje radical (la recta OF) de los círculos O₃ y O₈, debido a que con respecto a ABCD: SB.SC = SA.SD, luego S, F y O son colineales. De forma similar podemos probar que Q, E y O son colineales.

Entonces en el triángulo SOQ, SE y QF son alturas, donde P es su ortocentro, por lo tanto O es también el ortocentro del triángulo PQS. QED.

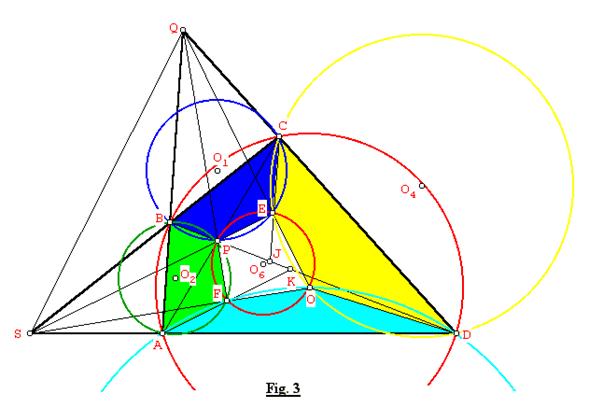
Corolario:

La recta que pasa por el circuncentro de un cuadrilátero cíclico y el punto de corte de sus diagonales es ortogonal a la tercera diagonal de dicho cuadrilátero.

Para nuestro caso, Ver Fig. 3: la tercera diagonal del cuadrilátero cíclico ABCD es QS, entonces la recta OP (no está dibujada) es ortogonal a QS, porque P es ortocentro del triángulo QSO.

Juan Carlos Salazar

caisersal@yahoo.com