Problema 168.-

Sea ABCD un cuadrilátero inscrito en un círculo O. El punto de corte de sus diagonales AC y BD es P, las prolongaciones de AB, DC y CB, DA se cortan en Q y S respectivamente. Probar que: O es el ortocentro del triángulo PQS.

Levi Shively PhD (1972): "Introducción a la Geometría Moderna" , Editorial CECSA, México, pag. 112.

Cuadrilátero completo

Un cuadrilátero completo lo forman cuatro rectas distintas,, tres de las cuales no son concurrentes y sus seis puntos de intersección. Las cuatro líneas son llamadas lados del cuadrilátero y los puntos son los vértices del cuadrilátero completo. Se llaman opuestos dos vértices que no están sobre el mismo lado. Los pares de vértices opuestos determinan tres líneas diagonales, en general no concurrentes, que forman el llamado triángulo diagonal.

Veamos una propiedad de este cuadrilátero completo.

Cuaterna armónica sobre un lado del cuadrilátero completo.

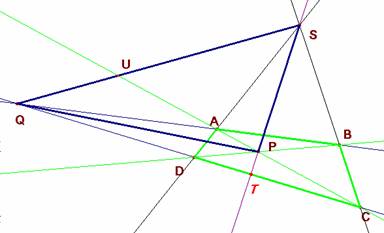 Si tenemos el cuadrilátero completo de vértices A, B, C y D y triángulo diagonal PQS. El punto T, proyección desde S del punto P sobre la recta QC es tal que la cuaterna formada por los puntos QTDC es armónica.

La propiedad es inmediata, sin más que considerar el triángulo DSC cortado por la transversal AB, y el mismo triángulo con las cevianas concurrentes en P. La aplicación sucesiva de los teoremas de Menelao y Ceva nos da:

(QDC)·(BCS)·(ASD)=1; (ADS)·(BSC)·(TCD)= —1;  multiplicándolas entre sí se obtiene: (QDC)·(TCD)= —1, que es lo que pretendíamos demostrar.

(La notación (JKL) representa la razón simple de estos puntos, es decir, (JKL) = )

Polar de un punto respecto de una cónica.

Si trazamos una recta que pase por un punto Q que no pertenece a una cónica dada, esta recta corta a la cónica, en general en dos puntos D y C.  El cuarto armónico de esa terna es un punto T de esa recta, que decimos que es el conjugado de Q respecto de la cónica.

Se llama polar del punto Q respecto de la cónica dada, al lugar geométrico de los conjugados de Q respecto de la cónica. Se prueba que este lugar geométrico es una recta.  Para determinarla se toman sobre la cónica cuatro puntos A, B, C  y D. Por la propiedad del cuadrilátero completo que hemos demostrado antes, el punto T es el conjugado de Q, respecto de la cónica situado en la recta CD y, por la invariancia de la razón doble por proyecciones, también es conjugado de Q el punto P, con lo que resulta que la polar de Q es la recta determinada por el lado SP del triángulo diagonal. Al punto Q se le llama polo de la recta SP.

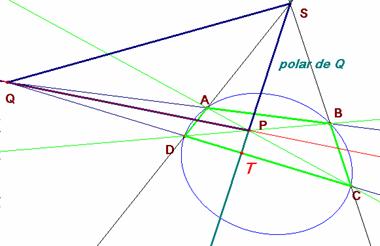Si T  es el cuarto armónico de la terna QDC  podemos decir igualmente que Q  es el cuarto armónico de la terna DCT o bien, que Q es el conjugado de T y por ello, la polar de T ha de pasar por el punto Q. Así pues, la relación de conjugación es simétrica, y por ello si un punto es el polo de una determinada recta (su polar), los puntos de ésta, tienen polares que pasan por su polo.

Lo que acabamos de ver es que el triángulo diagonal de un cuadrilátero completo sobre una cónica es un triángulo autopolar, es decir, que cada vértice es el polo del lado opuesto, y viceversa, cada lado de este triángulo es la recta polar del vértice opuesto. La polar de P es la recta QS, la de Q es la recta SP y por último, la de S es la recta PQ.

Diámetros de una cónica. Diámetros conjugados. Ejes.

En una cónica cualquiera, se llama centro de la misma al polo de la recta del infinito.

Cualquier recta que pasa por el centro es un diámetro de la cónica por definición. Cada diámetro corta a la recta del infinito en un punto. La polar de ese punto es otro diámetro, por tratarse de una recta que pasa por el centro, son los llamados diámetros conjugados. Si dos diámetros conjugados son perpendiculares, se dice que son los ejes de la cónica. En general, sólo hay un par de ejes en una cónica, salvo en el caso de la circunferencia en la cual, cualquier par de diámetros conjugados son ejes, pues son perpendiculares. Aceptando estos hechos tenemos para el problema en cuestión la siguiente situación:

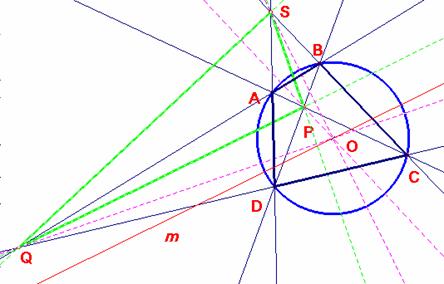
El triángulo PQS es el triángulo diagonal del cuadrilátero completo de vértices ABCD, por tanto es un triángulo autopolar.

Queremos demostrar que el diámetro OS es perpendicular al lado PQ. Bastará con probar que la recta m paralela a PQ por O es el diámetro conjugado del que pasa por S.  La recta m y su paralela PQ se encuentran en el punto del infinito R_∞ (PQ ∩m = R_∞ )_. La polar de R_∞, punto de la recta PQ, pasa por S (pues el triángulo PQS es autopolar) y por O (por estar en la recta del infinito), luego es el diámetro OS, y con esto se demuestra que OS es una altura del triángulo diagonal. Repitiendo el proceso con los otros vértices se concluye que O es el ortocentro.  c.q.d.