Problema 169
Propuesta de Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz).

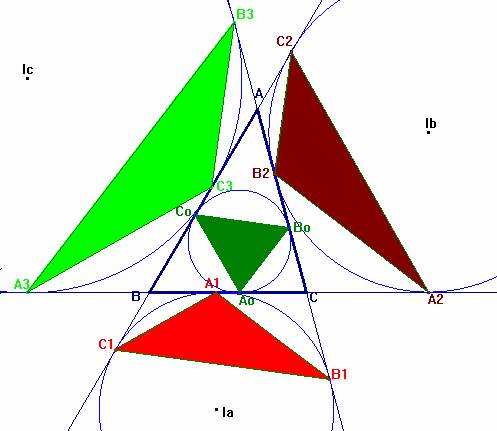
Dado un triángulo ABC se trazan sus circunferencias inscrita y exinscritas. Por los puntos de tangencia A₀ B₀ C₀ de la inscrita con el triángulo ABC se traza un triángulo de área S₀. Por los puntos de tangencia de cada circunferencia exinscrita con los lados se trazan tres triángulos A₁ B₁ C₁ de área S₁, A₂ B₂ C₂ de área S₂, A₃ B₃ C₃ de área S₃.
Demostrar que:
1/ S₀ = 1/S₁ + 1/S₂ + 1/S₃. (1)
Autor desconocido.

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

Notación:
2p = a +b +c (perímetro del triángulo ABC);
r, r₁, r₂ y r₃ son los respectivos radios de las circunferencias inscrita y exinscritas al triángulo ABC.
[ABC]= área del triángulo de vértices A, B y C.

Para probar el resultado enunciado, antes hemos de enunciar la siguiente propiedad que vamos a utilizar:
Se verifica la relación siguiente:

Para ver esto, observamos las siguientes igualdades entre áreas:

[ABC] + [BCI_a] = [ABI_a]+ [ACI_a] ;

Ahora bien, como:       [BCI_a] = a·r_1;  [ABI_a] = c·r_1; [ACI_a] = b·r₁

Tenemos que:              [ABC] = (-a + b + c )·r₁ = (p-a)·r₁

En definitiva: [ABC] = (p-a)·r₁

Del mismo modo, obtendríamos también: [ABC] = (p-b)·r₂ ;   [ABC] = (p-c)·r₃

Así, podemos relacionar:

ya que como se sabe: [ABC] = p·r

Probaremos ya a continuación la relación solicitada.

Para ello, determinamos los lados de los triángulos inscrito y exinscritos.

*En el triángulo inscrito, tenemos:

A₀B₀² = r² + r² -2r²·cos(p-C) = 2r²·(1+cosC)=2r²·2cos²C/2= 4r²·cos²C/2;

Es decir,           A₀B₀ =2r·cosC/2; y de forma análoga, B₀C₀ =2r·cosA/2; C₀A₀ =2r·cosB/2;

Luego el área del triángulo A₀B₀C₀ será:          S₀ =

*En el triángulo exinscrito de incentro I_a, tenemos:

B₁C₁² = r₁² + r₁² -2r₁²·cos(p-A) = 2r₁²·(1+cosA)=2r₁²·2cos²A/2 = 4r₁²·cos²A/2;

Entonces:         B₁C₁ =2r₁·cosA/2;

Sin embargo, para  A₁C₁² = r₁² + r₁² -2r₁²·cosB =2r₁²·(1-cosB)= 2r₁²·2∙sen²B/2 = 4r₁²·sen²B/2;
Así tenemos que: A₁C₁ =  2r₁· sen B/2; y, análogamente, A₁B₁ =  2r₁· sen C/2;

Luego el área del triángulo A₁B₁C₁ será:

S₁ = ;    

Mutatis mutandi para los triángulos A₂B₂C₂  y  A₃B₃C₃, tenemos que:

     

En definitiva, si desarrollamos cada uno de los miembros de la igualdad (1):

llegamos a los siguientes resultados:

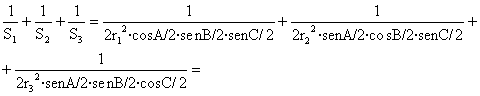
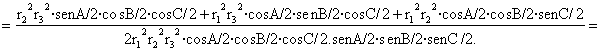
En definitiva, quedaría por identificar si es cierta la siguiente igualdad (2):

=   (2)

Para ver esto, tenemos en cuenta que:

¸ ¸ ,
entonces el segundo miembro de la igualdad (2) quedaría así:

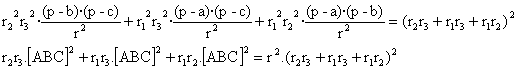
Vamos a demostrar, pues, que es cierta la siguiente igualdad (3):

 (3)

Teniendo de nuevo en cuenta:

[ABC] = (p-a)·r₁         [ABC] = (p-b)·r₂         [ABC] = (p-c)·r₃

           

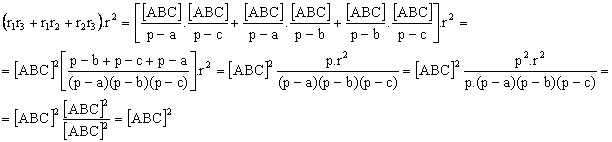
c.q.d.