Problema:

Problema 169:

Dado un triángulo ABC, se trazan sus circunferencias inscrita y exinscritas. Por los puntos de tangencia AoBoCo de la inscrita con el triángulo ABC se traza un triángulo de área S0. Por los puntos de tangencia de cada circunferencia exinscrita con los lados se trazan tres triángulos A1B1C1 de área S1, A2B2C2 de área S2 y A3B3C3 de área S3.

Demostrar que:

Demostración: Ver Fig. 1

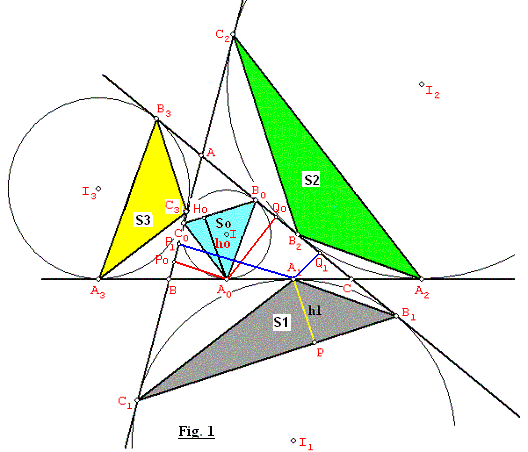
Sabemos que <C₀A₀B₀ +<C₁A₁B₁ = 180º, porque A₁B₁ y A₁C₁ son ortogonales a A₀B₀ y A₀C₀ respectivamente. Luego se cumple que:

… (1)

Además tenemos que los círculos (I₁) e (I), ambos son tangentes a las rectas AB, AC y BC. Por lo tanto, aplicaremos el teorema de Pappus,

Para el punto A₁ con respecto al círculo I₁:

A₁P₁.A₁Q₁ = A₁P², si A₁P₁ = d₁ y A₁Q₁ = d₂ y A₁P = h₁

h₁² = d₁.d₂……. (2)

Para el punto A₀ con respecto al círculo I, h₀es también la altura desde el vértice A₀:

h₀² = d₀₁.d₀₂…. (3)

Donde d₀₁ = A₀P₀ y d₀₂ = A₀Q₀ y h₀ = A₀H₀

Además conocemos que: BA₀ = CA₁ = (s-a) y BA₁ = CA₀ = (s-c)

Con

Como las distancias (perpendiculares) desde los puntos A₁ y A₀ hacia AB y AC conforman dos pares de triángulos rectángulos semejantes BP₀A₀ con BP₁ A₁ y AQ₀C con AQ₁C. Por semejanza de triángulos:

y , pero , entonces: