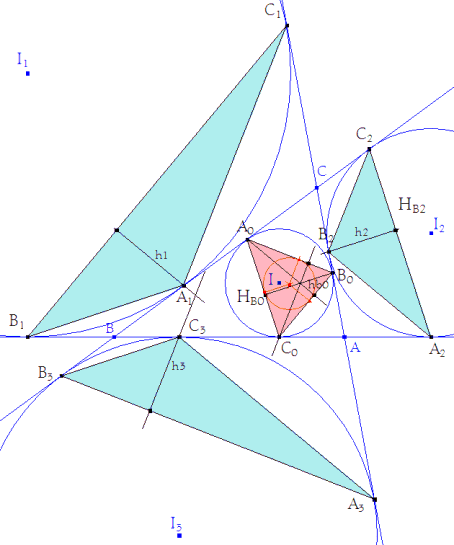
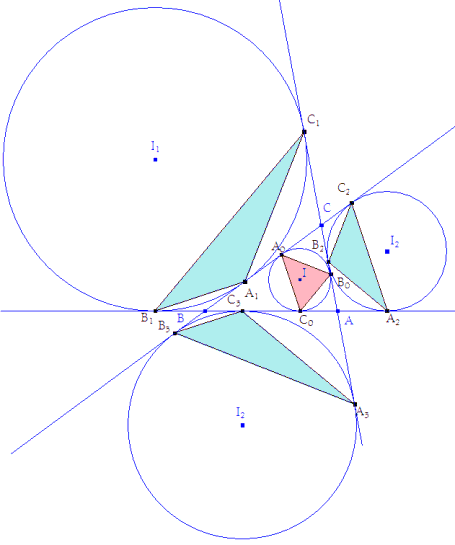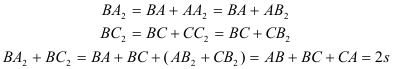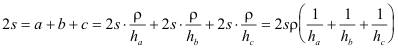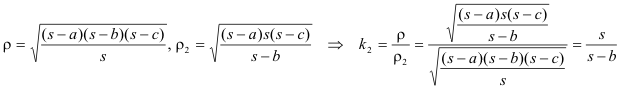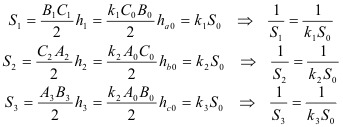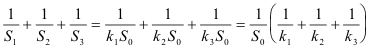Propuesta de Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz). Problema 171 y 169: En un triángulo ABC, con triángulos tangenciales externos A₁B₁C₁, A₂B₂C₂, A₃B₃C₃ y triángulo tangencial interno A₀B₀C₀. Demostrar que: 1/ρ₀ = 1/h₁ + 1/h₂ + 1/h₃ Donde: h₁, h₂ y h3₀ son alturas y r₀ es el inradio del triángulo A₀B₀C₀. Salazar, J.C. (2004): Propuesta personal Sea: S₀ el área del triángulo A₀B₀C_0. S₁ el área del triángulo A₁B₁C_1. S₂ el área del triángulo A₂B₂C_2. S₃ el área del triángulo A₃B₃C₃_. Demostrar que 1 / S₀= 1/ S₁ + 1/S₂ + 1/S₃. Autor desconocido. Solución de José María Pedret, Ingeniero Naval, Esplugues de Llobregat (Barcelona)

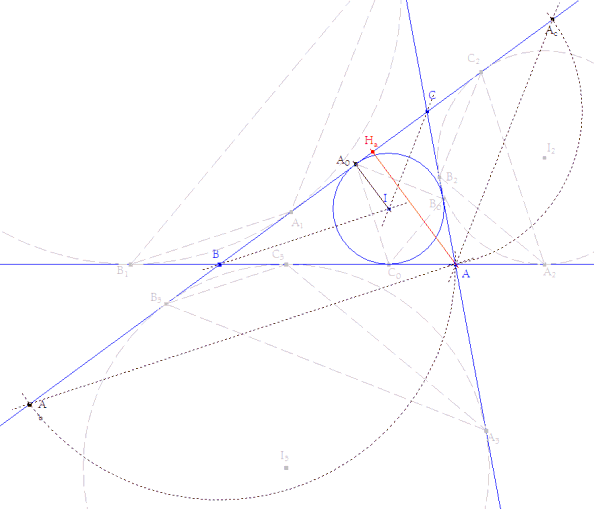
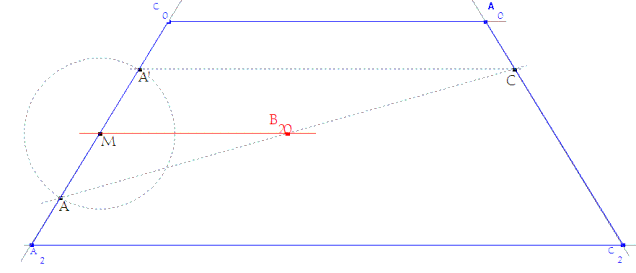
Dibujo del enunciado
figura 1
Marcha a seguir para la demostración
a)	Veremos la relación que existe entre el radio de la circunferencia inscrita y las tres alturas de un triángulo cualquiera.
b)	Aprovechando que los círculos ex-inscritos y el círculo inscrito son homotéticos. Relacionaremos las alturas de los triángulos tangenciales exteriores (1), (2), (3) con las alturas del triángulo tangencial interior (0).
c)	Combinaremos los resultados anteriores para concluir con el resultado buscado on los inversos de las alturas. (Correspondiente al problema 171)
d)	Con el resultado anterior (b) y (c) demostraremos el resultado pedido en el problema 169
Definiciones

a)	LAS TRES ALTURAS Y EL RADIO INSCRITO DE UN TRIANGULO CUALQUIERA
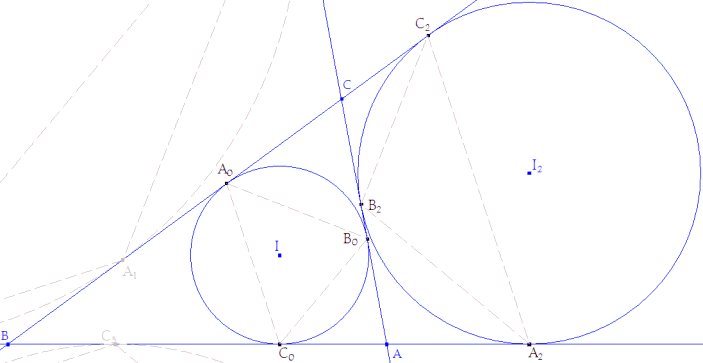
Con el fin de desarrollar la capacidad de observación de las figuras, el método usado, en este apartado, aprovecha las semejanzas de triángulos y las propiedades de los segmentos de las tangentes comunes a dos círculos. Con la construcción del enunciado, determinamos los puntos de contacto
figura 2
Teniendo en cuenta los triángulos que se forman con las bisectrices y partiendo de cada vértice hasta los puntos de contacto con el círculo inscrito Escribamos el perímetro como suma de los segmentos anteriores y apliquemos la igualdad de segmentos notando el semi-perímetro como s, nos queda en el círculo ex-inscrito y como seguimos observando y

Veamos ahora, los radios del círculo inscrito y el ex-inscrito
figura 3
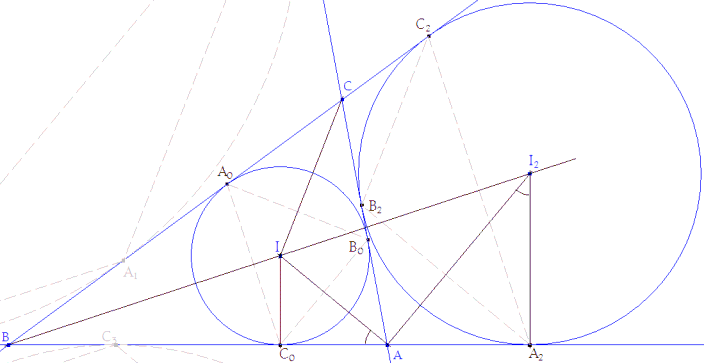
Triángulos a destacar de la figura, IC₀A, AA₂I₂. Estos triángulos son rectángulos y son semejantes y por tanto: Esta relación nos será muy útil más adelante. Al tener lados perpendiculares (ver marcas de ángulos en la figura), los triángulos rectángulos IC₀A, AA₂I₂ también son semejantes y Multiplicando las dos últimas ecuaciones obtenemos ρ y dividiendo obtenemos ρ₂

Ahora expresaremo figura 4 s las relaciones de las alturas

Sobre BC=a llevamos b=CA_c y c=BA_b, Como IB, IC son bisectrices de ABC, AA_c y AA_b son sus paralelas, entonces IBC y AA_bA_c son triángulos semejantes y por tanto:
expresión que nos permite expresar las alturas en función de los lados; pero nosotros expresaremos cada lado en función de lo anterior por tanto, en un triángulo cualquiera

b)	LAS ALTURAS DE LOS TRIANGULOS TANGENCIALES INTERIOR Y EXTERIOR
Ahora vemos que los círculos son homotéticos figura 5.0
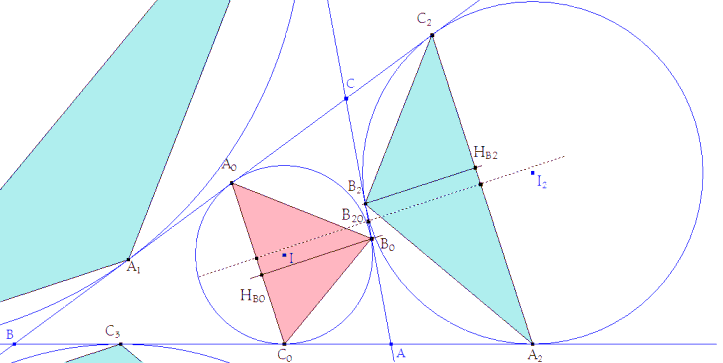
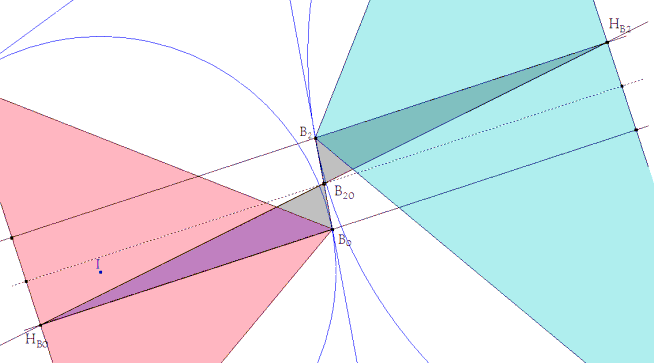
I e I₂ están sobre la bisectriz del ángulo B los extremos de radios perpendiculares a II₂ están, por ejemplo, en A₀ y en C₂ respectivamente y estos puntos están sobre BC, por lo tanto podemos decir que el círculo ex-inscrito es el transformado por una homotecia de centro B y razón la de los radios (aunque la razón no es necesaria hasta el final) Resultado ya obtenido al observar la figura 3. Al ser homotéticos C₂A₂ es paralela a A₀C₀,. Por B₀ trazamos la perpendicular B₀H_B0 a estas dos rectas que determina la altura h_b0. Por B₂ trazamos la perpendicular B₂H_B2 a estas dos rectas que determina la altura h₂.

B₂₀ el punto medio de B₀B₂ es el punto medio de CA=b/2 y equidista de las paralelas C₂A₂ y A₀C₀, Para ver la equidistancia sólo hay que observar la figura y recordar lo establecido en la figura 2 entonces A₀C₂A₂C₀ es un trapecio isósceles y como CC₂=C₀A y B₂₀ es el punto medio de CA, B₂₀ está sobre una paralela equidistante de las bases del trapecio
figura 5.1

entonces incluyendo este último resultado en la siguiente figura

figura 6
de donde los triángulos son simétricos respecto B₂₀ y por tanto y de aquí

c)	RELACION DE ALTURAS E INRADIO DE LOS TRIANGULOS TANGENCIALES (171)

figura 7
Si en el triángulo A₀B₀C₀, ρ₀ es el radio de su círculo inscrito (en rojo en la figura) , se cumple pero entonces c.q.d

d)	RELACION DE AREAS DE LOS TRIANGULOS TANGENCIALES (169)

Recordando la homotecia establecida entre el círculo inscrito y el ex-inscrito, tenemos tres homotecias de razones (figura 5) Expresando las áreas de los triángulos como base por altura, tenemos y de aquí sustituyendo hemos obtenido c.q.d