Problema 170
Propuesto por José María Pedret Ingeniero Naval. (Esplugas)
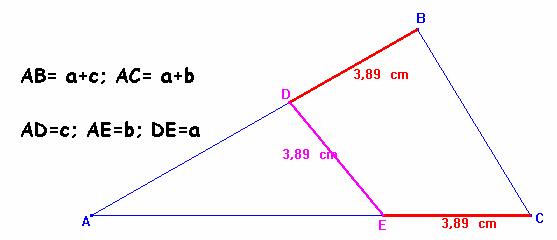
a) En un triángulo ABC, trazar una transversal que corta a AB en D y a CA en E de manera que BD = DE = EC.
Indicación: Inténtese predeterminar la forma de BXYC.

b) Por medio de lo anterior: Construir un triángulo ABC, conociendo el ángulo en A, la suma de lados a+b y la suma de lados a+c.

a = BC, b = CA, c = AB.

Petersen, J. . (1880-1990) . Métodos y Teorías para la Resolución de Problemas de Construcciones Geométricas.
Gauthier- Villars (1880) , Gabay, J. (1990), problema 179 , p. 33.

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

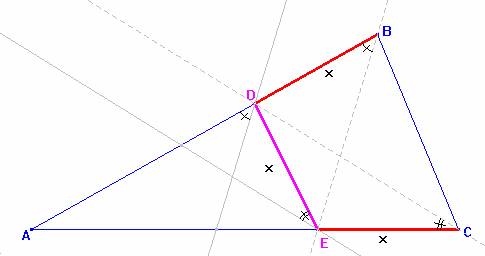
Supongamos el triángulo de lados b y c no iguales (b>c). En el caso de que b = c, entonces los puntos D y E serían los pies de las bisectrices interiores de los ángulos <C y <B, respectivamente.

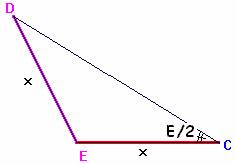
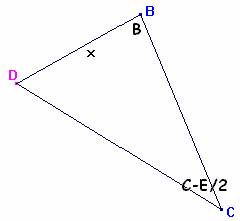
Consideramos los dos siguientes triángulos

Aplicando el teorema de los senos en ambos triángulos, resulta que:

DC : senE  = x : sen E/2

DC : senB  = x : sen(C-E/2)

Relacionando ambas expresiones, tenemos que:

DC : x = sen E : sen E/2 = sen B : sen (C-E/2), de donde:

2× cos E/2 × sen (C-E/2) = sen B

Transformando este producto en suma, llegamos a la relación: sen C + sen (C-E) = sen B sen (C-E) = sen B - sen C

Si bien esta relación la podemos simplificar teniendo en cuenta que

En definitiva:

sen (C-E) = (b-c) / 2R

Construcción a realizar:

1.- Construimos un triángulo rectángulo con uno de los catetos iguales a b-c y de hipotenusa 2×R, el diámetro de la circunferencia circunscrita al triángulo dado.

2.- Una vez construido el triángulo anterior el ángulo opuesto al cateto b-c será el ángulo C-E.

3.- Una vez determinado el ángulo C-E podemos obtener el ángulo E sin más que hacer
 C -(C-E)

4.- Ahora ya podemos construir el ángulo E/2 y trasladarlo al vértice C, haciendo coincidir una de los lados de dicho ángulo con el lado b. El otro lado del ángulo determinará al cortarse con el lado c el punto D.

5.- Una vez obtenido el punto D, podemos ya sin dificultad alguna trasladar la distancia BD = x sobre el lado AC, siendo CE = x.

b) Por medio de lo anterior: Construir un triángulo ABC, conociendo el ángulo en A, la suma de lados a+b y la suma de lados a+c.

Esta situación se solucionaría sin más que aplicando el apartado a) al triángulo construido de ángulo A y lados adyacentes a+b y a+c. Entonces trazando una transversal, según ya explicado en el apartado anterior, que corte a AB en D y a CA en E de manera que BD = DE = EC= a, obtendríamos así el triángulo ADE de lados cuyo ángulo en A sería el mismo y cuyos lados serían AD= b; DE= a y AE= c