|
Propuesto por José María Pedret Ingeniero Naval. (Esplugas) Problema 170 A) En un triángulo ABC, trazar una transversal que corta a AB en X y a CA en Y de manera que BX = YX = YC. Indicación: Inténtese predeterminar la forma de BXYC.
B) Por medio de lo anterior: Construir un triángulo ABC, conociendo el ángulo en A, la suma de lados a+b y la suma de lados a+c. a = BC, b = CA, c = AB.
Petersen, J. . (1880-1990) . Métodos y Teorías para la Resolución de Problemas de Construcciones Geométricas. Gauthier- Villars (1880) , Gabay, J. (1990), problema 179 , p. 33.
Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (BARCELONA) |
|
|
|
Establezcamos una guía general para resolver problemas de geometría. Esta guía deriva de los consejos que proporciona Julius Petersen en la Introducción de su obra. |
|
|
|
| • | Se buscará la solución del problema estudiando las relaciones geométricas existentes entre los elementos dados de la figura y los elementos buscados. |
• |
Empezaremos. EN TODOS LOS CASOS, por DIBUJAR UNA FIGURA que represente la solución buscada. Luego, sólo se trata de estudiarla a la luz de los teoremas de GEOMETRIA que conocemos. |
|
|
En muchas ocasiones, los problemas de geometría están compuestos por otros más simples que suelen reducirse a la determinación de un punto desconocido. Los siguientes pasos describen un método general para esta situación. |
|
• |
Se consideran aisladamente las dos condiciones que debe satisfacer el punto buscado.
A cada una de ellas corresponderá un lugar geométrico.
Si son rectas o círculos el problema está solucionado. Ya que, debiendo estar el punto buscado, al mismo tiempo, sobre cada uno de los dos lugares, estará en la intersección de ambos. (Cabri va más allá de rectas o círculos) |
• |
Se considera una de las condiciones impuestas a la figura como si no existiera.
Se buscarán, ahora, los lugares geométricos de los puntos de la figura que ahora quedará indeterminada. (Le falta una condición).
Se repetirá el proceso con cada condición. A veces, la simple re-incorporación de la condición ignorada nos da la solución sin necesidad de buscar más lugares. |
• |
De la figura trazada, se deducirá otra en la que la relación entre los elementos dados y los buscados se pondrá de manifiesto más cómodamente. |
Si los lugares geométricos no son sencillos o evidentes, añadiremos las siguientes reglas |
|
|
|
• |
Se introducen en la figura los elementos dados. Y se somete la figura a un examen atento para encontrar líneas y ángulos, que sin ser dados, pueden determinarse fácilmente a partir de los datos. |
• |
Se intentará descubrir una porción de la figura, determinada por los datos iniciales, que una vez trazada sirva para establecer el resto de la figura. De todas las posibles, se elegirá la que permita determinar la máxima porción de figura. |
• |
A menudo intentaremos BUSCAR TRIÁNGULOS que tengan tres elementos conocidos. |
|
|
APARTADO (A) |
|
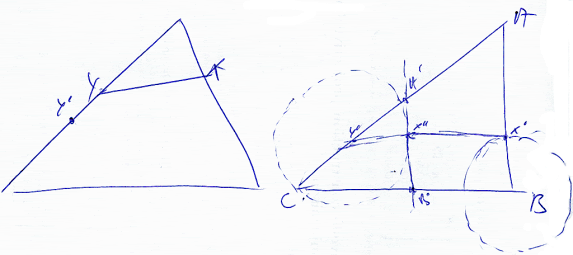 figura 00 |
|
Análisis previo.
Sea ABC el triángulo dado. Y en CA y X en AB
Trazamos la figura como si el problema estuviera solucionado. Si determinamos X ó Y el problema está solucionado.
El proceso general puede ser: |
|
1-2-3- |
Determinar el punto X. Imponer las condiciones del enunciado para determinar Y. Trazar la transversal pedida XY.
|
En la figura veremos que, en general, dos puntos Y’ en CA y X’ en AB con X’B=Y’C cumplen dos de las condiciones del problema; pero no cumplen la igualdad con XY. Si trasladamos X’ paralelamente a BC obtenemos X’‘ sobre el círculo de centro Y’ pasando por C.
X’‘ no es, generalmente, la solución; pero si es solución si la figura es otro triángulo A’B’C con B’C’ paralela a BC; y además B’X’Y’C tiene “la misma forma que” BXYC.
El enunciado dice BX=XY=YC; entonces, X estará en la intersección de dos círculos de igual radio, el primero de centro B pasando por X, el segundo de centro Y pasando por C.
El análisis del enunciado y la figura de estudio inicial nos indican la posibilidad de encontrar la solución por tres métodos: |
|
A.1 A.2 A.3 |
Determinación de X por un lugar geométrico sencillo. Determinación de X por una homotecia. Determinación de X por lugares geométricos complejos (lugar de cabri) |
|
|
A.1 Determinación de X por un lugar geométrico sencillo. |
|
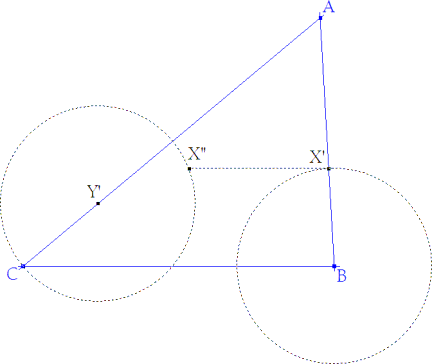 figura 01 figura 01 |
|
a) |
Empezamos el problema prescindiendo de una de las condiciones, por ejemplo que X está sobre AB.
Tomamos un punto variable Y’ sobre CA. Es claro que si Y’ fuera la solución, el punto X’ que le correspondería debería estar sobre el círculo de centro Y’ y radio Y’C. |
| b) |
Introduzcamos ahora la
condición descartada y prescindamos de la otra condición.
Si tomamos X' sobre AB con BX'=CY', en general X' no estará en el círculo de centro Y'. Pero si trazamos una paralela a BC desde X', cortará al círculo mencionado en X''. |
| Como la solución sólo se obtendría en el caso de que X' y X’‘ coincidiesen, nos preguntamos:
¿Cuál es el lugar geométrico del punto X’‘ si Y’ recorre CA?
Para determinar el lugar geométrico planteado, aplicaremos el “conocido método” de observar, observar, observar y observar la figura. |
|
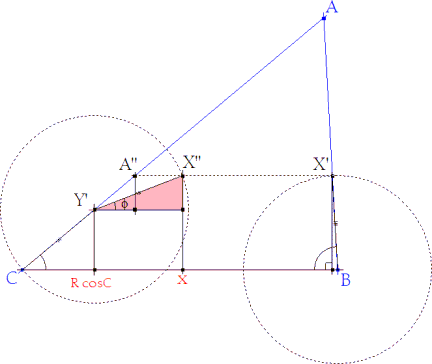 figura 02 figura 02 |
|
Simplificamos la búsqueda de relaciones en la figura con el uso de geometría analítica y trigonometría. Con una referencia ortogonal cartesiana: C como origen, BC como eje de abscisas y como eje de ordenadas, por C, perpendicular a BC.
La abscisa de X’‘
La ordenada de X’‘
La circunferencia de centro Y’ pasando por C
AL SER
|
|
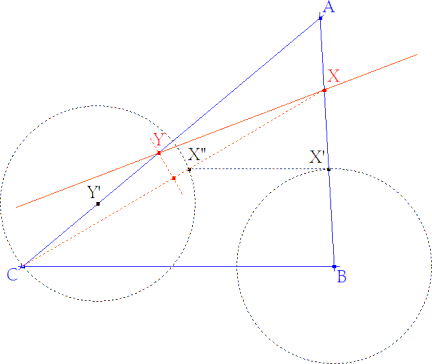 figura 03 figura 03 |
|
Cuando X’ coincide con B, Y’ coincide con C y por tanto esa recta pasará por C.
CX’‘ nos proporcionará X en su intersección con AB.
Como XY=CY, la mediatriz de CX corta en Y a CA.
Trazamos la transversal XY
|
|
A.2 Determinación de X por una homotecia. |
|
|
El enunciado nos ayuda cuando dice: “... Indicación: Intentemos determinar la forma de BXYC.” |
|
| • |
Los componentes de la solución deben tener una posición determinada respecto a los puntos y
líneas de la figura (en este caso, respecto al triángulo y en particular respecto a los vértices B y C).
En esta situación, lo mejor es hacer abstracción de una de las condiciones y obtener un sistema
de figuras semejantes y semejantemente dispuestas. Las figuras homotéticas cumplen esto de
forma sencilla. |
| • | En esta situación, los lugares geométricos de los puntos de las figuras son rectas que pasan por el centro de la homotecia; encontraremos , entonces, la figura buscada construyendo una figura cualquiera del sistema y luego su transformada por la homotecia que satisfaga la condición inicialmente dejada de lado. |
| • | La condición a ignorar inicialmente consiste generalmente en que una línea tenga una longitud determinada, que un punto deba estar en una línea determinada o que una línea deba pasar por un punto dado. |
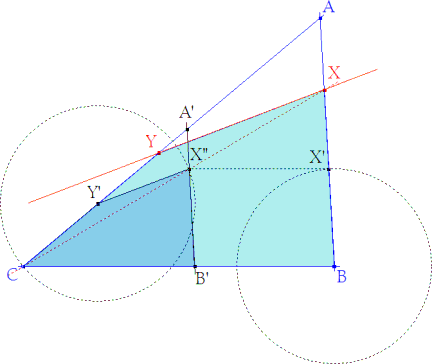 figura 04 figura 04 |
|
Utilizando parte de la construcción anterior (figura 01) e ignorando que el punto debe estar sobre la recta AB, obtenemos X’‘ por la traslación de AB paralelamente a BC.
Hemos construido la solución para un triángulo A'B'C transformado de ABC por una homotecia de centro C. Determinamos X, que por ser homotético de X'', estará sobre la recta desde el centro de homotecia C pasando por X''.
X está en la intersección de CX'' con AB y como el polígono B'X''Y'C es homotético a la solución, obtenemos la recta buscada trazando una paralela a Y'X''. Su intersección con CA nos da Y. |
|
|
|
A.3 Determinación de X por lugares geométricos complejos (lugar de cabri) |
|
 figura 05 figura 05 |
|
|
Volvamos al análisis inicial y consideremos
el círculo de centro Y' y el de centro B con radios iguales a CY'. El punto de
intersección Xi, de los dos círculos, sería solución si cumpliera, además, la
condición de estar sobre AB; en general no es así y por ello nos preguntamos
¿Cuál es el lugar geométrico del punto Xi si Y’ recorre CA?
Podemos contestar que el lugar es una cúbica. Imposible de determinar con regla y compás (excepto por puntos). Muy sencilla de determinar analíticamente. |
|
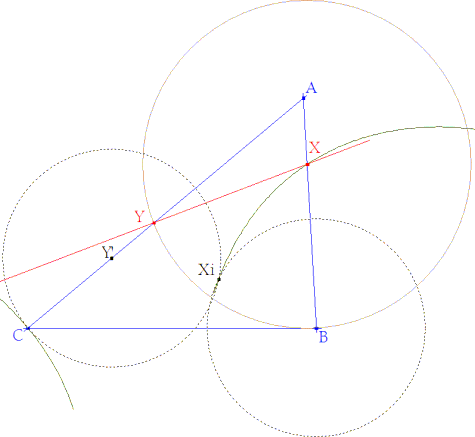 figura 06 figura 06 |
|
Con cabri II podemos usar la herramienta lugar que nos da la cúbica mencionada. Con cabri II plus podemos obtener, además, las intersecciones con ese lugar.
La intersección del lugar geométrico con AB nos proporciona X. la circunferencia de centro X pasando por B nos da Y en la intersección con CA. |
|
|
|
APARTADO (B) |
|
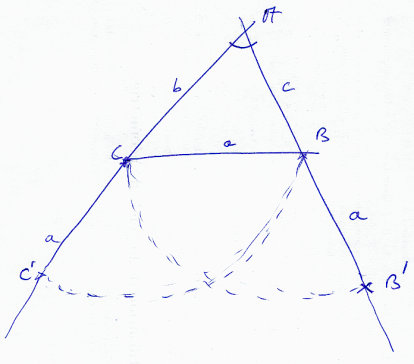 figura 07 figura 07 |
|
|
Análisis previo.
Dibujamos el triángulo ABC con a=BC, b=CA, c=AB.
Si con centro C y radio a trazamos un círculo corta a CA en A'. Si con centro B y radio a trazamos un círculo corta a AB en B'.
Observando la figura, vemos que a+b=C'A. a+c=AB' que junto con el ángulo en A son datos.
El polígono B'BCC' tiene tres lados iguales y dos de ellos sobre el triángulo AB'C'. Podemos reducir la determinación de BC al apartado (A).
AB'C' por ABC. B' por B. C' por C y al final será BC=a.
La única diferencia es que el triángulo original debe cumplir unas condiciones determinadas |
|
El enunciado: Construir un triángulo, conociendo A, a+b y a+c Se convierte en: Dados el un ángulo A cuyos lados miden a+b y a+c, determinar a. etc... |
|
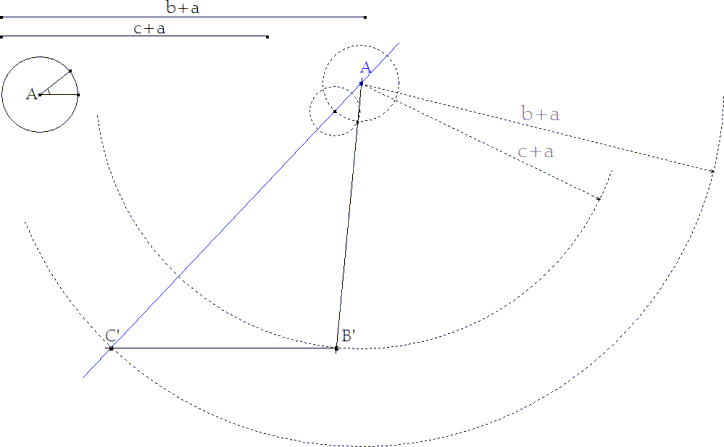 figura 08 figura 08 |
|
|
Sobre una recta cualquiera fijamos un
punto A.
Con vértice en A trazamos el ángulo A.
Sobre el primer lado determinamos C’ tal que C’A=a+b.
Sobre el segundo lado determinamos B’ tal que B’A=a+c.
Obtenemos el triángulo AB'C'. |
|
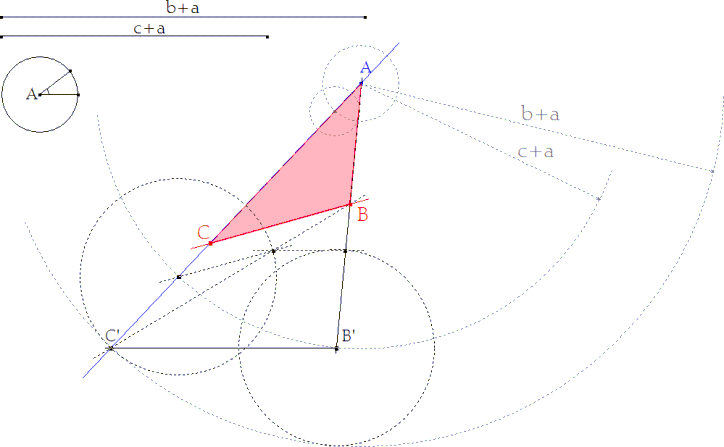 figura 09 figura 09 |
|
|
Tomando un punto cualquiera
sobre C'A, realizamos la construcción establecida en el apartado (A) y obtenemos
B y C de forma que:
a=BB'=BC=CC'=a
Hemos determinado el triángulo ABC de lados a, b, c y ángulo A en la intersección de b y c. |
|