Problema 171
En un triángulo ABC, con triángulos tangenciales externos A₁ B₁ C₁, A₂ B₂ C₂, A₃ B₃ C₃ y triángulo tangencial interno A₀ B₀ C₀ .
Demostrar que: 1/r₀ = 1/h₁ + 1/h₂ + 1/h₃
Donde: h₁, h₂ y h₃ son alturas y r₀ es el inradio del triángulo A₀B₀C₀.

Salazar, J.C. (2004): Propuesta personal

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

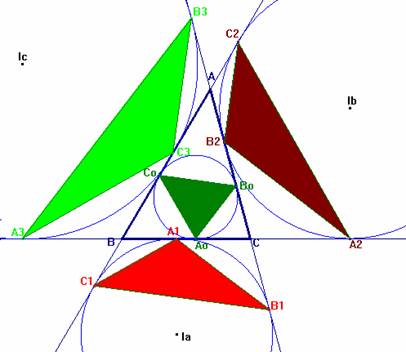
Notación:
2p = a +b +c (perímetro del triángulo ABC);
r, r₁, r₂ y r₃ son los respectivos radios de las circunferencias inscrita y exinscritas al triángulo ABC, y r₀ el inradio del triángulo A₀ B₀ C₀.
[ABC]= área del triángulo de vértices A, B y C.
Se sabe que:    [ABC] = (p-a)·r₁;       [ABC] = (p-b)·r₂ ;      [ABC] = (p-c)·r₃;        [ABC] = p·r

Probaremos a continuación la relación solicitada.

En el triángulo inscrito A₀B₀C₀, tenemos que:

A₀B₀² = r² + r² -2r²·cos(p-C) = 2r²·(1+cosC)=2r²·2cos²C/2= 4r²·cos²C/2;

Luego entonces:
A₀B₀ =2r·cosC/2; y de forma análoga, B₀C₀ =2r·cosA/2; C₀A₀ =2r·cosB/2;
Por tanto, el área del triángulo de semiperímetro 1/2×( A₀B₀ + B₀C₀ + C₀A₀ ) y de inradio r₀  será:

S₀=1/2×( A₀B₀ + B₀C₀ + C₀A₀ )×r₀ = 1/2×(2r·cosC/2+ 2r·cosA/2+ 2r·cosB/2)×r₀

También podemos expresar la anterior área como:

 

Así, tenemos que:

Por otro lado, en el triángulo tangencial externo A₁B₁C₁, y considerando la semejanza existente entre los triángulos AB₀C₀ y AB₁C₁, tenemos que:

            y como B₀C₀ =2r·cosA/2, tenemos por fin que:          

De igual modo para los otros dos triángulos tangenciales externos A₂ B₂ C₂ y A₃ B₃ C_{3 ,} determinamos los lados correspondientes a las alturas dadas h_i, i =1,2,3 del modo:

              y          .

Por tanto, sus áreas S_i vendrán dadas en función de h_i, como:
                       
                        S₁=1/2∙B₁C₁∙h₁;           S₂=1/2∙A₂C₂∙h₂;           S₃=1/2∙A₃B₃∙h₃

Por otro lado, sabemos (problema 169) que:

;     

;

;

y así:

Tenemos que probar:   1/r₀ = 1/h₁ + 1/h₂ + 1/h₃ , es decir:

 

o, equivalentemente:

Si tenemos en cuenta que:

¸ ¸

 la igualdad anterior equivaldrá a esta otra:

Como se sabe que:

[ABC] = (p-a)·r₁         [ABC] = (p-b)·r₂         [ABC] = (p-c)·r₃         [ABC]² = p×(p-a)(p-b)×(p-c)

la última expresión será equivalente a esta otra:

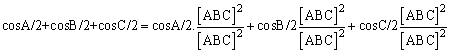
Igualdad esta última que es una identidad cierta sin más,  c.q.d.