Problema 172
Propuesto por
José Montes Valderrama, profesor del Centro Público de Adultos
·"Triana", Sevilla .
Sea el triángulo ABC, Ma, Mb, Mc, los puntos medios de sus lados y Ha, Hb, Hc,
los puntos de intersección de las semirrectas bisectrices de cada lado que
cortan a la circunferencia circunscrita, y no cortan a ninguno de los otros dos
lados. Siendo I el incentro de ABC, el triángulo HaHbHc corta a los segmentos
AI, BI y CI en los puntos A´, B´, y C´.
1.- El hexágono A´McB´MaC´Mb tiene la mitad de área que el triángulo ABC.
2.- Las diagonales A' Ma, y B'Mb se cortan en J. Demostrar que J pertenece a
C'Mc.
3.- J está en la recta que une el incentro I y el baricentro G del triángulo
ABC, verificándose
la relación: IJ=3 JG
Montes, J. (2004): Comunicación personal.
Solución de F. Damián Aranda
Ballesteros, profesor del IES Blas Infante de Córdoba.
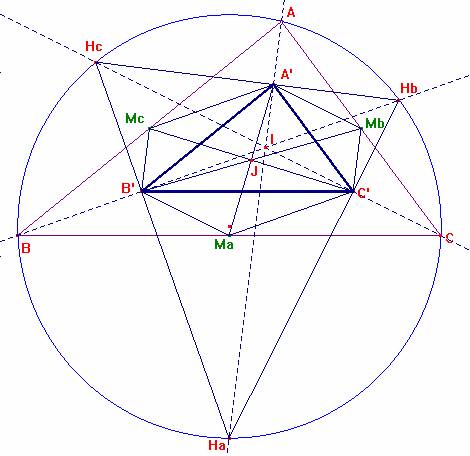
a) El hexágono A´McB´MaC´Mb
tiene la mitad de área que el triángulo ABC.
Con los datos del enunciado podemos deducir una serie de resultados destacados:
Los ángulos del triángulo Ha Hb
Hc son los siguientes:
<Ha= (B+C)/2; <Hb=
(A+C)/2; <Hc=
(A+B)/2
De esta manera, las rectas HaHb y HcC' se cortan perpendicularmente ya que el ángulo interior en C' de la circunferencia circunscrita al triángulo ABC es igual a la suma de los ángulos inscritos <Ha = (B+C)/2 y A/2. Por tanto suman p/2. De la misma forma sería perpendiculares las rectas HaHc y HbB' por un lado, y HbHc y HaA', por otro.
En definitiva, las rectas HaA', HbB' y HcC'
son alturas del triángulo Ha Hb Hc y, por
tanto se cortan en el punto I, que es el ortocentro de dicho triángulo. Así
resulta que el triángulo A'B'C' es el órtico del triángulo Ha Hb
Hc.
Por propiedad utilizada ya en el
Problema 166
Sean el círculo circunscrito a un triángulo HaHbHc
e I el punto de encuentro de las
alturas. Si se prolonga la altura Ha A' hasta A, se tendrá: IA' = A'A.
(Se precisa que A' es el punto de corte
de la altura desde Ha con el lado HbHc o su prolongación. A es el punto de corte de
la altura con la circunferencia circunscrita.)
Utilizando esta propiedad, tenemos que:
2×IA' =IA; 2×IB'
=IB; 2×IC' =IC;
Así el triángulo A'B'C' es el homotético del original ABC con centro de homotecia el punto I (=incentro del ABC y ortocentro del Ha Hb Hc) y razón k=1/2.
Así, el triángulo A'B'C' es congruente con el medial del ABC, es decir, con el Ma Mb Mc.
En el triángulo IAB resulta que A' y B' son puntos medios de IA e IB, luego B'Mc es la paralela media del lado IA, luego el segmento B'Mc es paralelo y de igual longitud que el segmento IA'. Por tanto el cuadrilátero IB'McA' es un paralelogramo de área igual a 2×[IA'B'].
De igual modo, [IA'MbC']= 2×[IA'C'] y también [IB'MaC']= 2×[IB'C']
Luego la suma de todas ellas será igual al área del hexágono A´McB´MaC´Mb, es decir:
[A´McB´MaC´Mb]= 2×[IA'B']+ 2×[IA'C']+ 2×[IB'C'] = 2×[A'B'C']= 2×1/k2×[ABC]= 1/2[ABC]
b) Las diagonales A' Ma, y B'Mb se cortan en
J. Demostrar que J pertenece a C'Mc.
Como McMa es la paralela media al lado AC en el triángulo
ABC, y A'C' es también la paralela media al lado AC en el triángulo IAC,
resulta que el cuadrilátero McMaC'A' es un paralelogramo
y las diagonales se cortan en su punto medio J. En concreto este punto J es el
mismo punto medio de los otras diagonales A'Ma, y B'Mb del paralelogramo
A'MaB'Mb.
c) J está en la recta que une el
incentro I y el baricentro G del triángulo ABC, verificándose la relación: IJ=3
JG.
Como ya se ha probado en el apartado anterior, el punto J ejerce de centro de simetría del triángulo A'B'C' respecto del MaMbMc y así ocurrirá también con los respectivos baricentros G' y G de ambos triángulos. Señalemos que el punto G, baricentro del triángulo ABC es el mismo baricentro para su triángulo medial MaMbMc .
Por tanto, se darán las siguientes relaciones vectoriales a considerar:
*De la homotecia de centro I y k=1/2, tenemos que:
, es decir G' es el punto medio del segmento IG.
*Por la simetría de centro el punto J, tenemos que:
, es decir el punto J es el punto medio del segmento GG'.
Relacionando ambos hechos, tenemos que:
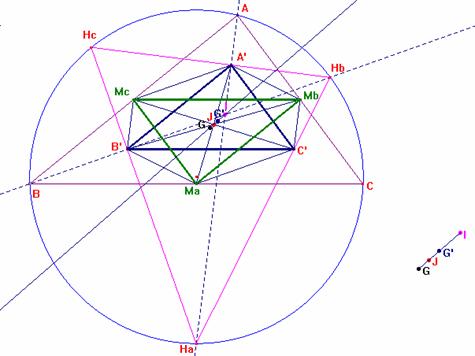
