Problema 172

Sea el triángulo ABC, Ma, Mb, Mc, los puntos medios de sus
lados y Ha, Hb, Hc, los puntos de intersección de las semirrectas
bisectrices de cada lado que cortan a la circunferencia circunscrita,

y no cortan a ninguno de los otros dos lados

Siendo I el incentro de ABC, el triángulo HaHbHc corta a los segmentos AI, BI y CI en los
puntos A´, B´, y C´.

1.- El hexágono A´McB´MaC´Mb tiene la mitad de área que el
triángulo ABC.

2.- Las diagonales A' Ma, y B'Mb se cortan en J. Demostrar que J pertenece a C'Mc.

3.- J está en la recta que une el incentro I y el baricentro G del triángulo ABC, verificándose la
relación: IJ=3 JG

Montes, J. (2004): Comunicación personal.

 Solución por José Montes Valderrama, profesor del Centro Público de Adultos “Triana” de Sevilla.

No cabe duda de que H_a, H_b y H_c se sitúan en los puntos medios de

Por esta razón las rectas AH_a, BH_b, y CH_c, son las respectivas bisectrices de los ángulos inscritos A, B y C, quedando el incentro I determinado por la intersección de estas bisectrices.

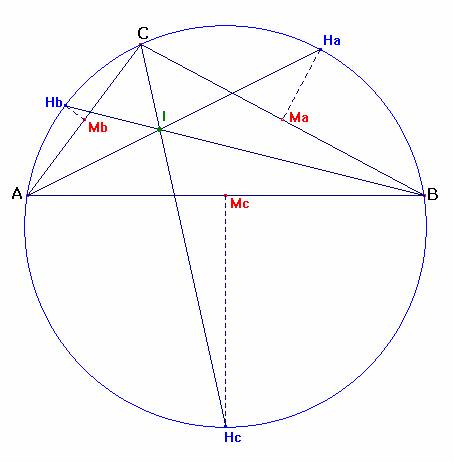El triángulo H_aH_bH_c corta a los segmentos AI, BI y CI en los puntos A´, B´, y C´.

    

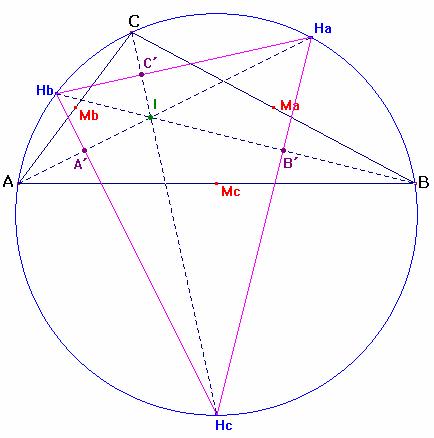
PRIMERA PARTE

        El hexágono A´M_cB´M_aC´M_b tiene la mitad de área que el triángulo ABC.

       

TEOREMA 1

A´ está en el punto medio del segmento AI

Para ello, basta demostrar que H_c es el circuncentro del triángulo BIA.

       

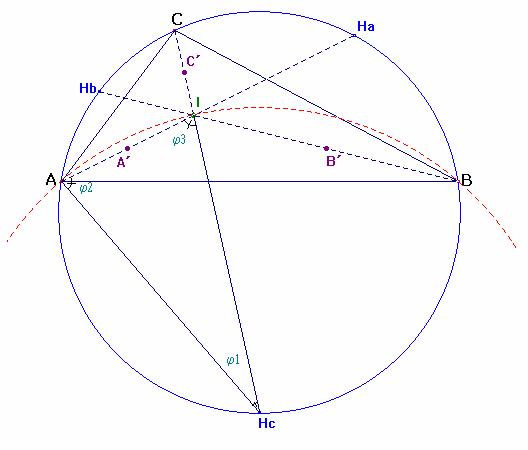
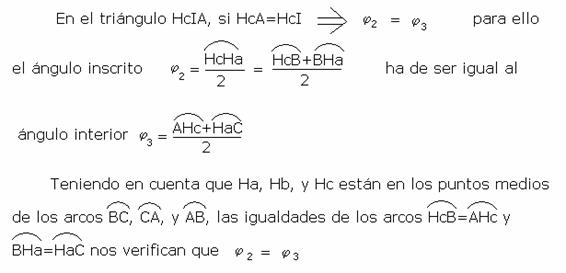
 Con este teorema queda también probado que B´está en el punto medio de BI. Con análogo procedimiento, es decir, demostrando que H_a es el circuncentro del triángulo CIB, o bien H_b lo es de AIC, se determina que C´es el punto medio de CI.

TEOREMA 2

Las diagonales de un paralelogramo se dividen entre sí en dos partes iguales

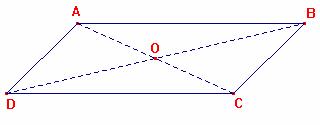
En los triángulos AOB, COD

1.   AB=CD

2. <OAB=<OCD  (ángulos alternos)

3. <OBA=<ODC  (ángulos alternos)

Por tanto, los triángulos AOB y COD son congruentes. En particular,

AO=OC

BO=OD

TEOREMA 3

El segmento que une los puntos medios de dos lados de un triángulo es paralelo al tercer lado, y es igual a la mitad del mismo.

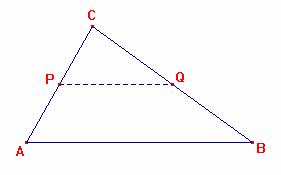
        Si P y Q son respectivos puntos medios de AB y BC, entonces

1.  PQ es paralelo a AB

2.  PQ= AB

        Si se construye una paralela por B a AC hasta cortar en R la prolongación de PQ, se tiene

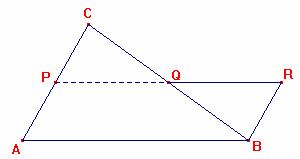
1. <PCQ=<QBR (ángulos alternos)

2. <CPQ=<QBR (ángulos alternos)

3.   CQ=QB (por hipótesis)

        Por tanto los triángulos CPQ y QBR son congruentes. En concreto

CP=RB   y   PQ=QR  es decir  PQ= PR

Pero   CP=PA, por tanto PA=RB.

        Al ser, por construcción, PA y RB  iguales y paralelos, y ser unidos por sus extremos por sendas líneas rectas; “son también ellas mismas iguales y paralelas” (Proposición 33. Libro I). Luego

PQ es paralelo a AB y también PQ= PR  , de lo que se deduce

PQ= AB

        Aplicando este teorema 3 al triángulo AIC

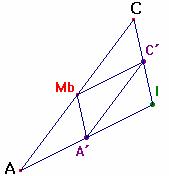
se tiene una partición en cuatro triángulos congruentes AA´M_b, A´IC´, M_bC´C y C´M_bA´.

        Y haciendo extensivo este razonamiento a los triángulos BIA y CIB, se obtiene

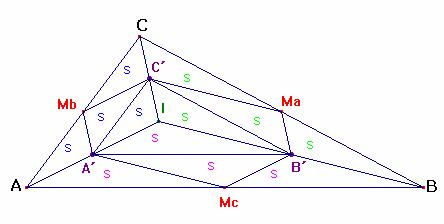
una partición del triángulo ABC en 12 triángulos iguales cuatro a cuatro, y puesto que el hexágono contiene 6 triángulos iguales dos a dos, su área es la mitad que la del triángulo ABC.

SEGUNDA PARTE

J es el punto de intersección de las diagonales M_aA´, M_bB´, M_cC´. Además, J está en la recta que une el incentro I y el baricentro G del triángulo ABC, verificándose la relación:

IJ=3 JG

J es la intersección de M_aA´, M_bB´y M_cC´

1. M_bC´ es paralelo a M_cB´

Teniendo en cuenta que “las paralelas a una misma recta son también paralelas entre sí” (Proposición 30. Libro I) se infiere que al ser en triángulo AIC, por el Teorema 3, M_bC´paralelo al lado AI  y a su vez, en el triángulo BIA, AI paralelo M_cB´, entonces M_bC´es paralelo a M_cB´.

2.  M_bC´=M_cB´

Por el Teorema 3, en triángulo ABC, M_bM_c es paralelo a BC y en el

 

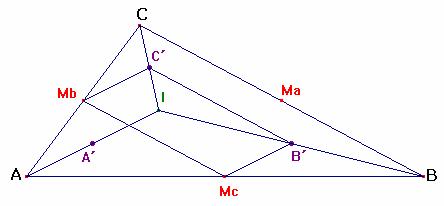
triángulo CIB, C´B´es paralelo a BC. Por tanto, M_bM_c es paralelo a C´B´, determinándose el paralelogramo M_bM_cB´C´, y por ello M_bC´=M_cB´.

3. Diagonal compartida

De las consideraciones anteriores se tiene un hexágono los lados paralelos e iguales dos a dos, que admite en su interior la construcción de tres paralelogramos de la forma

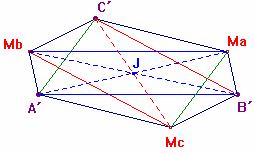
Teniendo en cuenta el teorema 2, en el paralelogramo M_bA´B´M_a, J es el punto medio de las diagonales M_aA´y M_bB´, pero J también es el punto medio de las diagonales M_cC´y M_bB´ en el paralelogramo M_bM_cB´C´.

 Por  compartir ambos paralelogramos la diagonal M_bB´, J  pertenece a la diagonal M_cC´.

I,J,G están alineados y se verifica IJ=3JG

Para última parte del problema, que se hará mediante la geometría analítica, hacen falta las coordenadas de dos vértices opuestos del hexágono, situándose en su punto medio J  1.

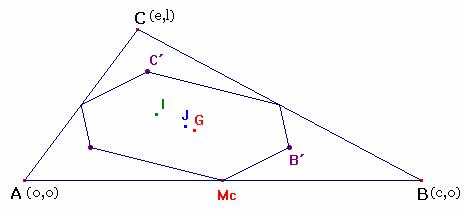
        Siendo:

       

       

la bisectriz interior de A :      

la bisectriz interior de B :

de cuyo sistema de ecuaciones se obtienen las coordenadas del incentro:

I ( , )

Las coordenadas de C´ quedarían determinadas por el punto medio de I y C( ):

C´[ , ]

J es el X(1125) de la ETC

También J es el punto medio entre C´ y M_c( , ):

J [ , ]

Sólo falta el baricentro:

G( , )

Haciendo el cálculo con los cuadrados de las distancias:

[ ]

]

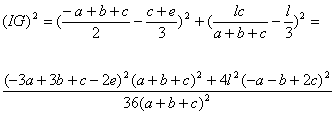
Se cumple entonces que:

 Þ

Þ  lo cual prueba que los puntos I, J, G están alineados.