Para el aula
Problema 173
32.- Relaciones entre los lados y los ángulos de un polígono.
Principiando por el triángulo designaremos por a, b , c las magnitudes absolutas de los lados, por A, B C los ángulos opuestos, según se acostumbra en trigonometría; tomemos por origen el vértice del ángulo
C y por eje el lado CB, suponiendo que el vértice del ángulo A está á la parte superior.... dos fórmulas conocidas:
| a=c cos B + b cos C |
c sen B = b sen C |
que pueden servir para determinar dos de las cinco cantidades que entran en ellas cuando las otras tres sean conocidas, determinándose el sexto elemento del triángulo por la ecuación A+B+C = pi.
Domínguez, M. (1879): Elementos de Geometría Analítica. Edición del autor. Madrid. p. 29
Solución de Maite Peña Alcaraz, alumna del Colegio Portaceli de Sevila (26 de mayo de 2004)
La segunda parte de la fórmula, csenB=bsenC es una consecuencia inmediata del teorema del Seno, que dice que a/senA=b/senB=c/senC; y que se demuestra tomando un triángulo cualquiera y aplicando la obtención del seno de unángulo a los triángulos rectángulos que se obtienen con una de las alturas.
La primera parte se obtiene si trazamos la altura sobre el lado a:
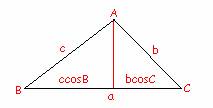
basta aplicar las fórmulas de sen B= cateto contiguo/hipotenusa y cos C= cateto contiguo/hipotenusa, válidas en los triángulos rectángulos.
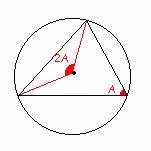
Para demostrar que los ángulos de un triángulo suman 180º, usaremos las propiedades de los arcos capaces. Un triángulo siempre se puede inscribir en una circunferencia, por tanto la suma de los ángulos centrales (360º) es la mitad que la suma de los ángulos interiores, esto es 180º