Problema 175.-

En un triángulo ABC es AB=AC. D es el punto medio de BC. E es el pie de la perpendicular trazada por D a AC. F es el punto medio de DE. Demostrar que AF es perpendicular a BE.

Larson, L.C. (1990): Problem-solving through problems.

Problem books in Mathematics, Edited by P.R. Halmos. Springer Verlag. (p. 27)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

Consideraremos para nuestro propósito, el sistema de referencia afín métrico determinado por el punto D, como origen de referencia y los lados BC y AD como los ejes x e y, respectivamente. Según este sistema de referencia, los anteriores puntos tienen las siguientes coordenadas:

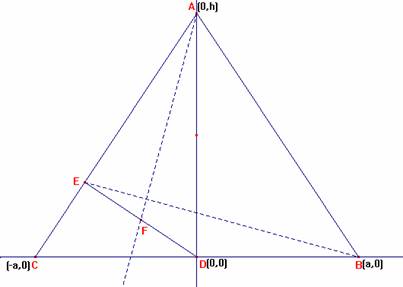El punto E pertenece a las rectas AC y DE cuyas ecuaciones respectivas son:

Recta AC: hx - ay +ah =0

Recta DE: ax + hy =0

Resolviendo el sistema proporcionado por estas ecuaciones obtenemos las coordenadas del punto E:

y, por consiguiente F, punto medio del segmento DE, será:

*Consideramos el vector

Este vector es paralelo al .

*Por otro lado, el vector es paralelo a este otro .

Como c.q.d.