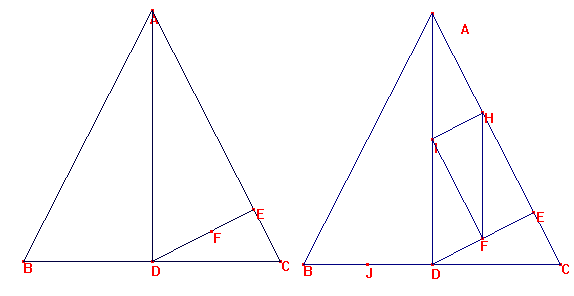
En un triángulo ABC es AB=AC. D es el punto medio de BC.

E es el pie de la perpendicular trazada por D a AC.

F es el punto medio de DE.

Demostrar que AF es perpendicular a BE.

Larson, L.C. (1990): Problem-solving through problems.

Problem books in Mathematics, Edited by P.R. Halmos. Springer Verlag. (p. 27)

Gúsiev V. y otros (1989). "Problemas Matemáticos. Geometría". Ed. Mir. Moscou. Problema 455. página 90. (Referencia ofrecida por Ricard Peiró i Estruch profesor de Matemáticas del IES 1 de Xest (València), a quien el editor agradece la cita.)

Solución del editor.

Dado ABC isósceles y D punto medio de BC con DE perpendicular

a AC.Consideremos la paralela media IH en ADE:

A continuación por J, punto medio de BD tracemos la perpendicular a BC y por A tracemos la

perpendicular a AB, ambas se cortan en N: NIF están alineados, pues NI es paralelo a AH y IF es a AE.

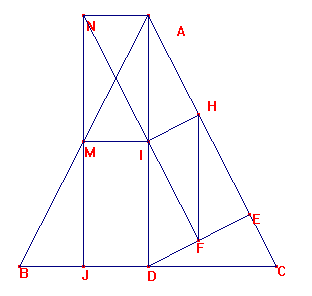
Ya que NI es paralelo a MD y MD es paralelo también a AC.

N es el centro de la circunferencia circunscrita a BDE, pues está a igual distancia de los tres vértices:

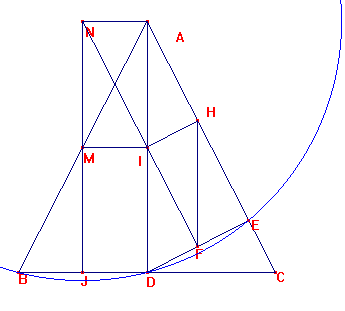
Consideremos P, punto medio del radio ND.

Será:

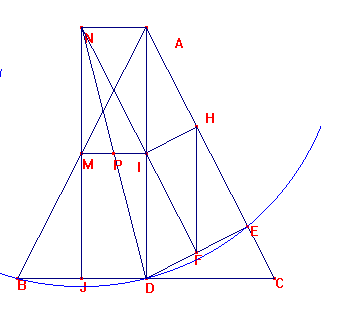
PJ=PD=PA, por ser P punto medio de las diagonales del rectángulo ANJD

Además al ser NFD triángulo rectángulo, la mediana PF=PD=PN.

Así, P es centro de la circunferencia circunscrita al triángulo AFJ:

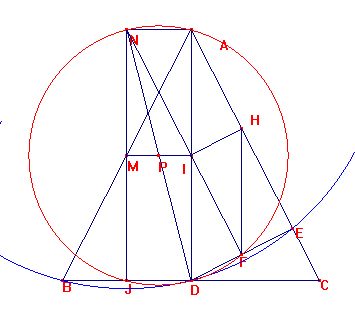
Tal circunferencia también pasa por N y D. AJ es diámetro de la

misma.

Luego AFJ es triángulo rectángulo, y FJ es perpendicular a AF.

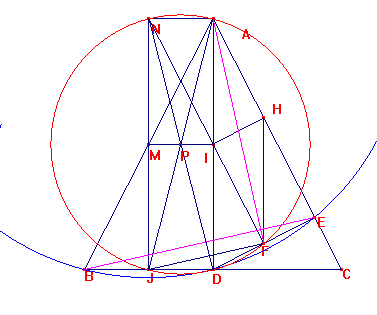
Por último, al ser los triángulos DFJ y DEB semejantes es FJ paralelo

a BE y por ello, cqd, es BE perpendicular a AF.

Ricardo Barroso Campos.

Didáctica de las Matemáticas.

Universidad de Sevilla