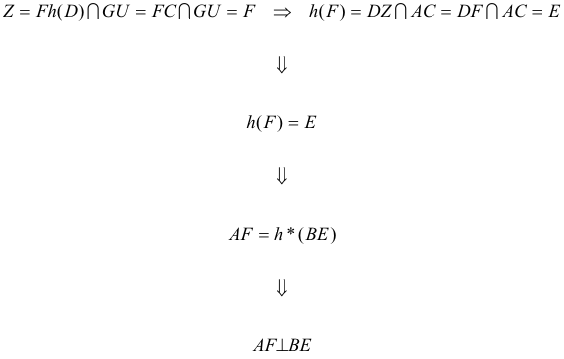Problema 175.- En un triángulo ABC es AB=AC. D es el punto medio de BC. E es el pie de la perpendicular trazada por D a AC. F es el punto medio de DE. Demostrar que AF es perpendicular a BE. Larson, L.C. (1990): Problem-solving through problems.Problem books in Mathematics, Edited by P.R. Halmos. Springer Verlag. (p. 27) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). |
|
|
|
INTRODUCCION |
|
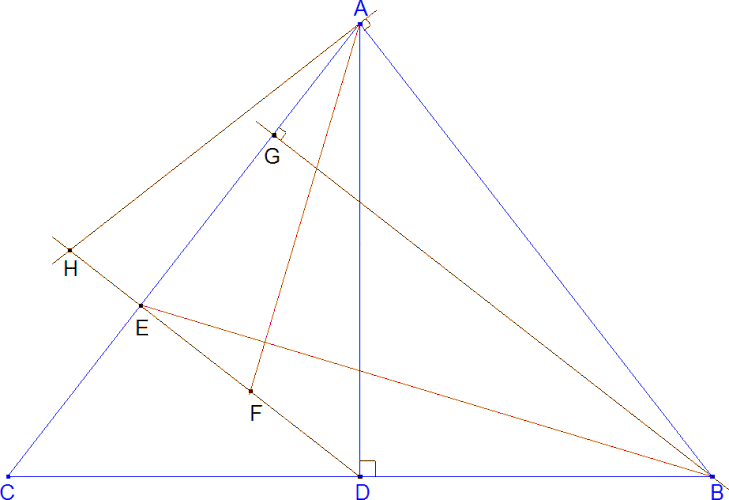 Figure 1 Figure 1
|
|
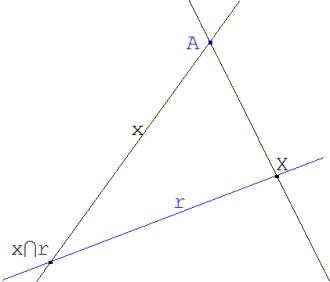
El dibujo del enunciado lo traduciremos en un primer paso como : Fijados ABC y D con AB=AC y D punto medio de AB, dibujar la recta DE perpendicular a AC y E la intersección de ambas. Además de F punto medio de ED trazamos: |
|
|
la recta BG perpendicular a AC y G la intersección de ambas y la recta AH perpendicular a AB y H la intersección con ED |
El estudio del dibujo nos muestra que hay muchas rectas por B y muchas rectas por A y que esas rectas guardan “alguna” relación. Estudiar esa relación y determinarla nos permitirá relacionar BE con AF y comprobar lo que solicita el enunciado. Intentaremos resolver esas cuestiones en el campo de la GEOMETRIA PROYECTIVA. |
|
|
|
Las herramientas “proyectivas” para la resolución de este problema pueden encontrarse en el problema 137 de estas páginas que nos ofrece RICARDO BARROSO CAMPOS: PLANTEAMIENTO Observando la figura vemos que por el punto fijo B pasan las rectas BA, BG, BC y BE. Y los puntos A, G, C y E están sobre AC. Observando la figura vemos que por el punto fijo A pasan las rectas AH, AC, AD y AF. Y los puntos H, C, D y F están sobre DE. Sabemos seguro (pues así las hemos construido) que:
Vemos que la relación mencionada en la INTRODUCCION es la relación de perpendicularidad de las rectas del haz B* (conjunto de las rectas que pasan por B) y las rectas del haz A*. Hemos definido una homografía:
No hay duda de que es una homografía pues está inducida por una transformación lineal de rectas vectoriales en rectas vectoriales (la suma de dos vectores rotados π/2 es la rotación de π/2 de la suma de dichos vectores) y es biyectiva (desde un punto exterior a una recta sólo puede trazarse una perpendicular). Además, está perfectamente definida pues conocemos la imagen de tres rectas distintas. |
|
¿Qué ocurre entre BE y AF? Si comprobamos que
|
|
|
|
|
|
DESARROLLO Y RESOLUCION Del resumen proyectivo del problema 137 recordamos: |
|
13 |
Homografías entre Rectas Proyectivas y Haces de Rectas |
En un plano proyectivo, existe una biyección canónica p entre una recta proyectiva dada r y un haz dado A*; a todo punto X de r se le asocia la recta AX de A* y a toda recta x de A* se le asocia el punto x ∩ r. Esta biyección conserva la razón doble [10]. p recibe el nombre de proyección de r sobre A* y su inversa la de A* sobre r. |
|
|
|
h*(AX) = AX’ = p(X’) = poh(X) = pohop-1(AX). Como h→pohop-1 es isomorfismo de grupos, podemos trabajar indistintamente con una homografía de puntos de una recta o con una homografía de rectas de un haz. |
|
|
|
|
|
Paso de los haces proyectivos a rectas proyectivas |
|
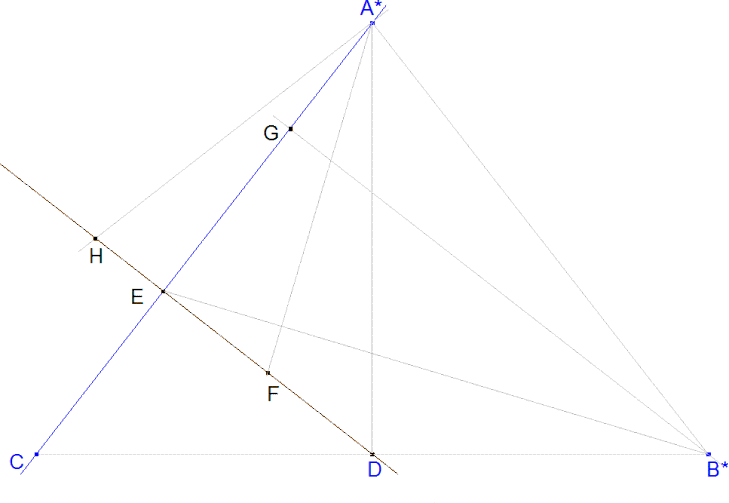 Figure 3 Figure 3
|
|
Gracias al isomorfismo anterior, en nuestro caso, trasladaremos nuestro problema a la siguiente homografía:
|
|
y lo que tenemos que comprobar es:
|
|
|
|
Recordemos también que: |
|
08 |
Eje de Homografía: Construcción Geométrica de la Imagen de un Punto |
Sea h: r→r’ una homografía entre rectas proyectivas. Si h es una proyección, dados dos puntos A y B de r, AB’ y BA’ se cortan en una recta fija que pasa por r ∩ r’. Si h no es una proyección, AB’ y BA’ se cortan sobre la recta que une h(r ∩ r’) y h-1(r ∩ r’). Esta recta se llama eje de homografía. |
|
|
|
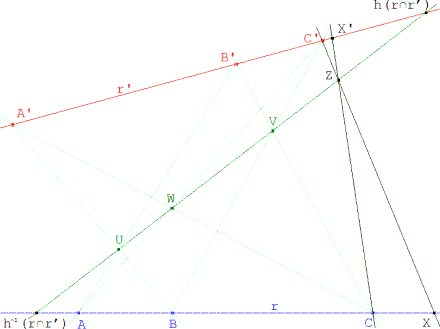
Para construir el eje de homografía UV, determinamos U = AB’ ∩ BA’ y V = BC’ ∩ CB’. (podemos comprobar que W = CA’ ∩ AC’ está sobre el eje.) Para construir la imagen de un punto X de r, hallamos Z = XC’ ∩ UV y así, X’ = CZ ∩ r’. |
|
|
|
Determinación del eje de homografía en nuestro caso |
|
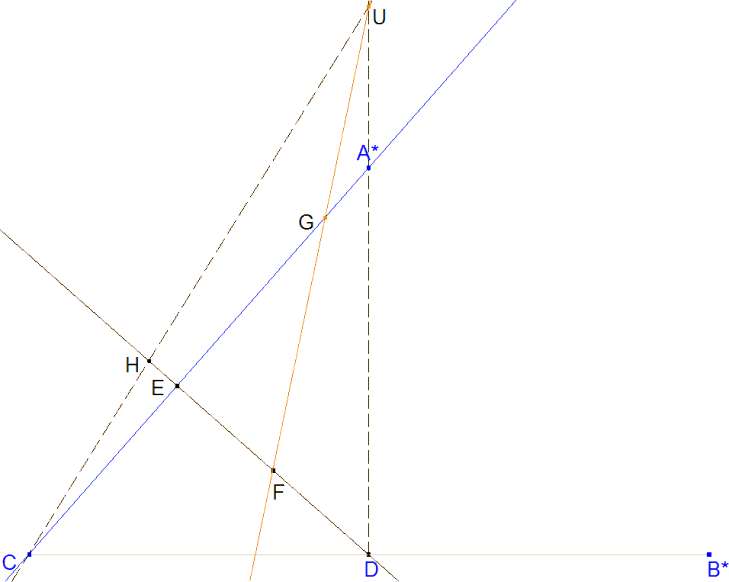 Figure 5 Figure 5
|
|
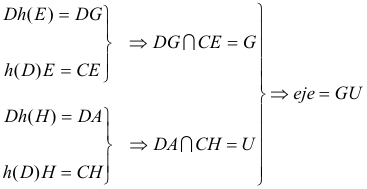
y además es fácil comprobar que
|
|
|
|
Construcción de la imagen de F Recordemos que: Para construir la imagen de un punto X de r, hallamos Z = XD’ ∩ UV y así, X’ = DZ ∩ r’. En nuestro caso:
Por lo tanto
c.q.d. |
|
|
|
|
|