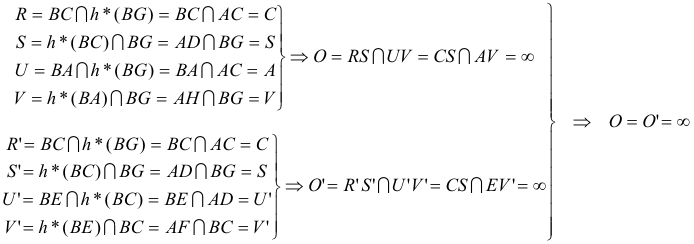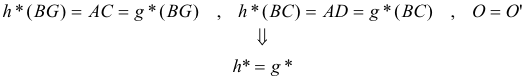Problema 175.- En un triángulo ABC es AB=AC. D es el punto medio de BC. E es el pie de la perpendicular trazada por D a AC. F es el punto medio de DE. Demostrar que AF es perpendicular a BE. Larson, L.C. (1990): Problem-solving through problems.Problem books in Mathematics, Edited by P.R. Halmos. Springer Verlag. (p. 27) Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona). |
|
|
|
INTRODUCCION |
|
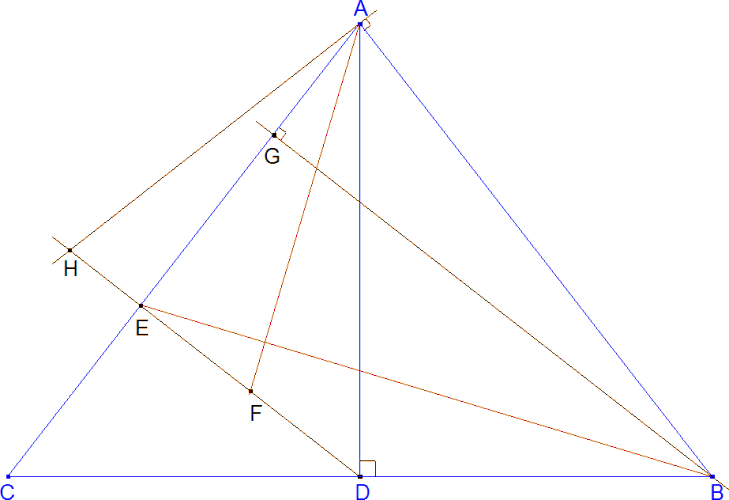 Figure 1 Figure 1
|
|
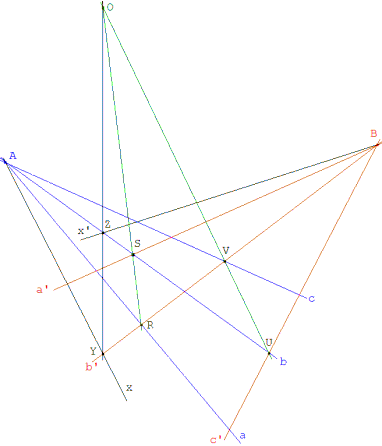
El dibujo del enunciado lo traduciremos en un primer paso como : Fijados ABC y D con AB=AC y D punto medio de AB, dibujar la recta DE perpendicular a AC y E la intersección de ambas. Además de F punto medio de ED trazamos: |
|
|
la recta BG perpendicular a AC y G la intersección de ambas la recta AH perpendicular a AB y H la intersección con ED |
El estudio del dibujo nos muestra que hay rectas por B y rectas por A y que esas rectas se cortan. Estudiar el comportamiento de las intersecciones de las rectas por B con las rectas por A y relacionarlas con la intersección de BE y AF nos permitirá comprobar lo que solicita el enunciado. Intentaremos resolver esas cuestiones en el campo de la GEOMETRIA PROYECTIVA. |
|
|
|
Las herramientas “proyectivas” para la resolución de este problema pueden encontrarse en el problema 137 de estas páginas que nos ofrece RICARDO BARROSO CAMPOS: PLANTEAMIENTO Observando la figura vemos que por el punto fijo B pasan las rectas BA, BG, BC y BE. Observando la figura vemos que por el punto fijo A pasan las rectas AH, AC, AD y AF. Definimos dos homografías entre haces de rectas dando las imágenes de tres rectas:
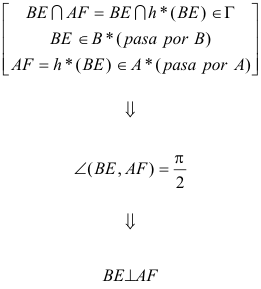
Demostraremos que h*=g*. Para ello veremos que además de coincidir en las rectas BG y BC, tienen el mismo centro de homografía. Con el teorema de CHASLES STEINER veremos que la cónica proyectiva descrita por la intersección de los rayos homólogos de la homografía h* es la circunferencia de diámetro BA Como g*=h* la cónica proyectiva definida por g* es la misma circunferencia de diámetro BA y por lo tanto la intersección de BE y g*(BE) ( o lo que es lo mismo de BE y AF) estará sobre esa circunferencia. Y como BE y AF pasan además por los extremos del diámetro, sabemos que forman un ángulo recto ¡ y por lo tanto son perpendiculares! |
|
|
|
DESARROLLO Y RESOLUCION Del resumen proyectivo del problema 137 recordamos: |
|
12 |
Centro de Homografía |
Sea h*: A*→B* una homografía. Si h* es una proyección, para todo par de rectas r y s de A*, la recta que une r ∩ h*(s) con s ∩ h*(r) pasa por un punto fijo de la recta AB; si h* no es una proyección las rectas que unen r ∩ h*(s) con s ∩ h*(r) pasan por el punto h*-1(AB) ∩ h*(AB). Este punto es el centro de homografía. |
|
|
|
Para construir el centro de homografía, determinamos RS con R = a ∩ b’ y S = b ∩ a’, determinamos UV con U = b ∩ c’ y V = c ∩ b’. Como las dos rectas RS y UV pasan por el mismo punto fijo, este punto estará en su intersección O = RS ∩ UV. |
|
|
|
|
|
Determinación de los centros de homografía y de la igualdad de h* y g* |
|
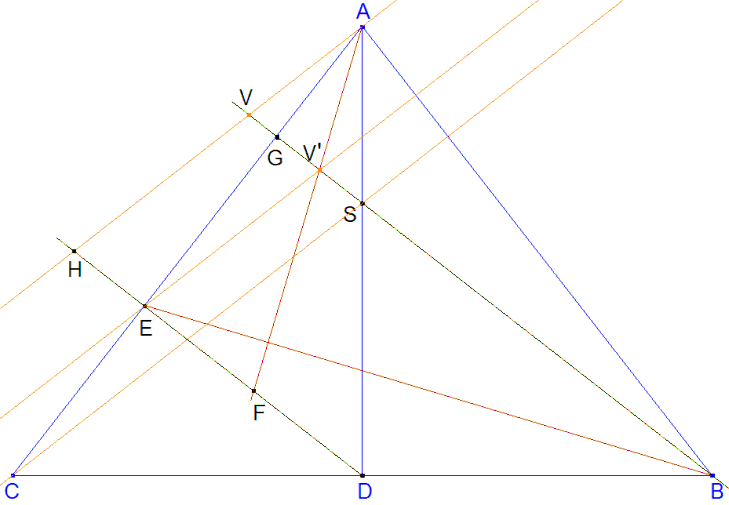 Figure 3 Figure 3
|
|
Recordemos: Para el centro de homografía, determinamos RS y UV con R = a ∩ b’, S = b ∩ a’, U = b ∩ c’ y V = c ∩ b’. Como RS y UV pasan por el mismo punto fijo, este punto estará en su intersección O = RS ∩ UV.
Resultado que podíamos prever porque S es el ortocentro de ABC, V’ es el punto medio de S y G y V está sobre AH y entonces CS, AH y EV’ son paralelas. |
|
|
|
Y como
|
|
|
|
Determinación de Γ la cónica asociada a h* Recordemos ahora el teorema de Chasles Steiner: |
|
17 |
Descripción de una cónica. Teorema de Chasles Steiner |
...Teorema de Chasles Steiner. Un primer enunciado: Una homografía entre haces de rectas define una cónica y recíprocamente. Avanzando un poco más, decimos que si C es de la cónica, entonces la biyección AC→BC es una homografía. |
|
|
|
Teorema de Chasles Steiner. Un segundo enunciado Dados A y B dos puntos distintos del plano proyectivo y la homografía entre haces de rectas concurrentes h: A*→B*; si a es una recta del haz A* entonces el lugar de a ∩ h(a) es una cónica.... |
|
18.02 |
Tangentes a la cónica definida por una homografía. |
h(AC) = BC, h(AD) = BD, h(AE) = BE Por definición de h, h(AB)= BB y h-1(BA)= AA. ¿Eso que significa? Para responder, usamos el centro de homografía. Determinación de h(AB) AB corta a las rectas de B* en B, el otro punto buscado está sobre BO, entonces h(AB) = BO. Pero BO sólo tiene un punto en común con la cónica y ese punto es B. h(AB) = BO es la tangente a la cónica en el punto B. Determinación de h-1(BA) BA corta a las rectas de A* en A, el otro punto buscado está sobre AO, entonces h-1(BA) = AO. Pero AO sólo tiene un punto en común con la cónica y ese punto es A. h-1(BA) = AO es la tangente a la cónica en el punto A. |
|
29 |
Dual del Teorema de Steiner |
Sean a y b dos tangentes a una cónica. La polar p del punto a ∩ b corta a las tangentes a, b en los punto A, B. Una tangente cualquiera distinta de a y de b, corta a a y b en X y X’. La biyección de a sobre b definida por A →a ∩ b, a ∩ b →B, X →X’ es una homografía de eje p. Recíprocamente, sea h de a sobre b una homografía de rectas proyectivas. El eje p de esta homografía corta a y b en A y B. Entonces para todo punto X de a, la recta Xh(X) envuelve a una cónica tangente en A y B a a y b. |
|
|
|
|
|
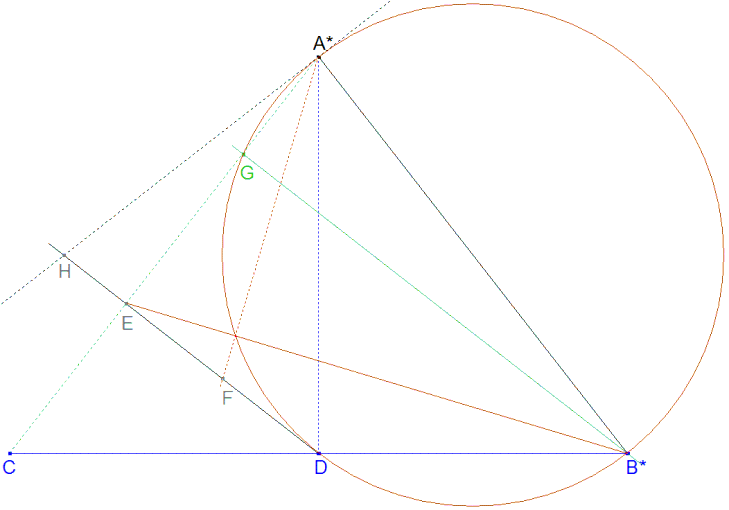 Figure 5 Figure 5
|
|
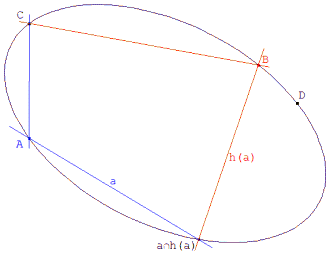
De lo anterior: Si tenemos cinco puntos entre los cuales no hay tres alineados podemos definir una cónica y sólo una que pase por esos cinco puntos [18.01]. Pero aprovechando la dualidad podemos también determinar la cónica por cuatro puntos y la tangente en uno de ellos, o tres puntos y las tangentes en dos de ellos. etc. En nuestro caso, tenemos cuatro puntos (A, B, G, D) y una tangente AH. Tenemos pues determinada la cónica Γ. |
|
|
|
Conclusión G está sobre Γ. BG es perpendicular a AG (forman un ángulo recto) y pasan respectivamente por A y B; D está sobre Γ. BD es perpendicular a AD (forman un ángulo recto) y pasan respectivamente por A y B. A está sobre Γ. BA es perpendicular a AH=AA (forman un ángulo recto) y pasan respectivamente por A y B. Vemos claro que la cónica Γ ES UN CÍRCULO definido como el lugar geométrico de los vértices del ángulo recto cuyos lados pasan respectivamente por A y B. Entonces:
c.q.d. |
|