Problema 175

En un triángulo isósceles , , sea D el punto medio del lado

Sea E el  pie de la perpendicular al lado  que pasa por el punto D.

Sea F el punto medio del segmento .

Probar que  y  son perpendiculares.

Solución de Ricard Peiró i Estruch profesor de Matemáticas del IES 1 de Xest (València)

Solución 1:

Consideremos el triángulo  con las siguientes

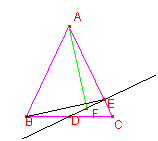
coordenadas cartesianas:

. Entonces, .

La recta r que pasa por los puntos A, C té ecuación: .

La recta s que pasa por el punto D i es perpendicular al lado  té per ecuación:

.

El punto E es la intersección de les rectas r, s:

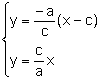. Entonces, .

F es el punto medio del segmento . Entonces, .

Calculemos las componentes de los vectores .

Calculemos el producto escalar de los vectores :

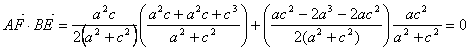
Entonces,  son perpendiculares.

Solución 2

Sea .

Aplicando el teorema de Pitágoras al triángulo :

Los triángulos  son semejantes, aplicando el teorema de Tales:

. Por tanto, ,   .

Aplicando el teorema de Pitágoras al triángulo :

,       

Efectuemos el producto0 escalar y comprobemos que es cero.

 

     

    

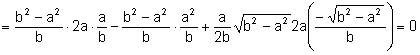
Entonces,  son perpendiculares.