Problema 175.-

En un triángulo ABC es AB=AC. D es el punto medio de BC.

E es el pie de la perpendicular trazada por D a AC.

F es el punto medio de DE.

Demostrar que AF es perpendicular a BE.

Larson, L.C. (1990): Problem-solving through problems.

Problem books in Mathematics, Edited by P.R. Halmos. Springer Verlag. (p. 27)

Gúsiev V. y otros (1989). "Problemas Matemáticos. Geometría". Ed. Mir. Moscou. Problema 455. página 90. (Referencia ofrecida por Ricard Peiró i Estruch profesor de Matemáticas del IES 1 de Xest (València), a quien el editor agradece la cita.)

Notas y solución de Mark Tudosi.

Este problema es fácil, pero uno hay cierta geometría difícil en él.

Probablemente algunas soluciones proyectivas lo cubren, es duro para mí, pero voy a dar unas pequeñas observaciones.

Se sabe que cuando un triángulo se mueve en un plano permaneciendo semejante a sí mismo, y dos vértices se mueven en líneas rectas (o circunferencias), el tercer vértice también se mueve en una línea recta (o circunferencia).

En este problema el vértice A está fijo, el vértice I se mueve sobre BC, y el J sobre DE, y <IJA=90, moviéndose de ABD a ADE permaneciendo semejante, (el ángulo A no cambia).

Hay una posición AGF cuando IJ es paralela a BE y tiene lugar cuando GF es la línea media. 

Por este motivo se selecciona F en el problema.

 Esto hace que AF sea perpendicular a DE.

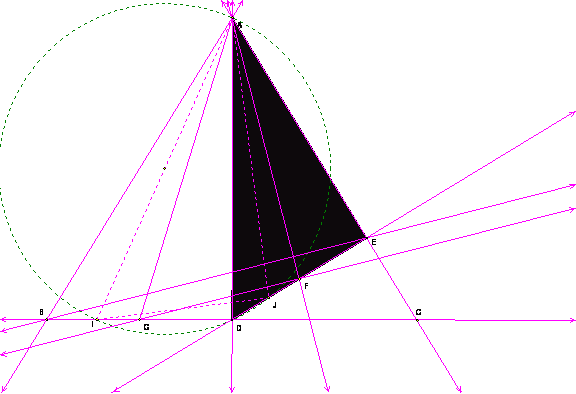
No puedo dejar de comentar otra “observación”.

 Es casi una demostración sin palabras.

 Como se puede ver en el dibujo, las líneas paralelas hacen todo semejante y el diámetro de la circunferencia media es la suma de radios de la pequeña (roja) y grande (azul).

Así todo en esta circunferencia es media aritmética de objetos semejantes en las otras dos.