Problema 176 Extra.-
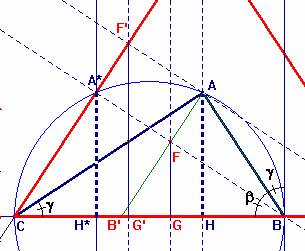
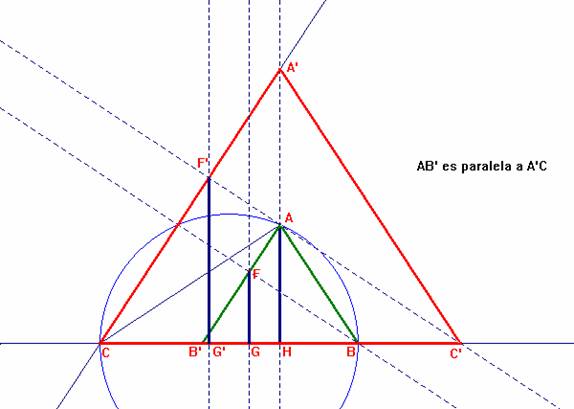
Sea un triángulo ABC, rectángulo en A y no isósceles. Sean los puntos B' y C' los simétricos de B y C, respectivamente, según el eje AH siendo H el pie de la perpendicular trazada desde A al lado BC. Construimos los triángulos ABB' y A'CC' siendo A' tal que AB' sea paralelo a A'C, y A' sobre la recta AH. Sean BF y C'F' las alturas de los vértices B y C' en BAB' y C'AC. Por F y F' tracemos FG y F'G' perpendiculares de F y F' sobre BC. Probar que AH es media aritmética de los segmentos FG y F'G'.

Romero, J.B. (2004) Comunicación personal. In memoriam Miguel de Guzmán Ozámiz

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

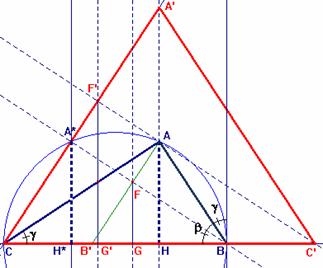
Destacamos los siguientes hechos de interés:	La recta BF corta perpendicularmente a la recta CA’, pues esta es paralela, por construcción a la recta AB’. Por tanto, el punto de corte A* pertenecerá a la circunferencia de diámetro BC. Tenemos además que <A*CA = <ABA* por abarcar la misma cuerda AA*. Por tanto, el triángulo ABC y A*CB son simétricos respecto de la mediatriz del diámetro BC. Se tendrá, pues, que A*H*=AH Por otro lado los triángulos A*BC y FBB’ son semejantes. Luego será cierta la igualdad: ®
	El punto A pertenece a la recta CF’ ya que como el triángulo ABB’ es isósceles, entonces el ángulo en A medirá p-2b=2g. Como <HAB = <HAB’, entonces <HAB = <HAB’= g y así: <BAC’ =<HAC’-<HAB= b-g . <BAC’= b-g Del mismo modo, <F’AC=<F’AB’-<CAB’=p/2-(b-g); <F’AC=2g En definitiva, en A se verifica que: <BAC’+ <BAC + <F’AC = p, ya que: <BAC’+ <F’AC= b - g + 2g = g. Por tanto, los puntos C’, A y F’ están alineados. De este hecho, obtenemos que los triángulos CC’F’ y CA*B y BAC son semejantes entre sí. En concreto: ®
Sumando ambas expresiones, obtenemos: En definitiva, AH es la media aritmética de los segmentos FG y F’G’, c.q.d.