PROBLEMA 176
In memoriam.- Homenaje del profesor Juan Bosco Romero Márquez a Miguel de Guzmán Ozámiz(1936-2004)
Sea un triángulo ABC, rectángulo en A y no isósceles.
Sean los puntos B' y C' los simétricos de B y C, respectivamente, según el eje AH
siendo H el pie de la perpendicular trazada desde A al lado BC.
Construimos los triángulos ABB' y A'CC' siendo A' tal que AB' sea paralelo a A'C, y A' sobre la recta AH.
Sean BF y C'F' las alturas de los vértices B y C' en BAB' y C'AC.
Por F y F' tracemos FG y F'G' perpendiculares de F y F' sobre BC.
Probar que AH es media aritmética de los segmentos FG y F'G'.
Romero, J.B. (2004) Comunicación personal.
SOLUCIÓNSolución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú :
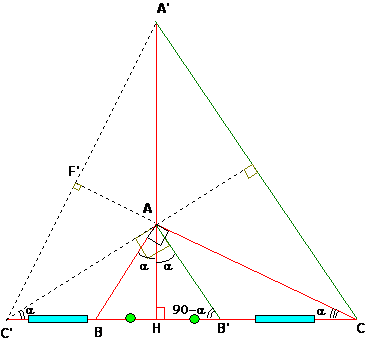
En el triángulo ABB’ (isósceles)
ÐBAH=ÐHAB’=α entonces ÐACB’=α
EN triángulo CAC’: como AH es mediatriz entonces AC’=AC
Luego ÐAC’B=ÐACB’=α entonces ÐC’AB’=90º y como AB’//A’C entonces
Al prolongar El segmento C’A cota al segmento AC formando un ángulo de 90º
Finalmente en el triángulo C’A’C (A es el ortocentro) luego C’, F’ y A’ son colineales.
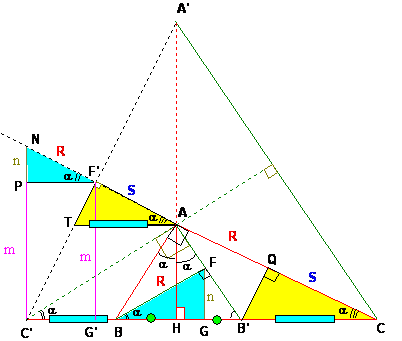
Levantamos la perpendicular C’N a C’C por C’
En el triángulo rectángulo NC’C se cumple que NA=NC
Del gráfico C’TAB (paralelogramo) entonces TA=C’B luego los triángulos
TF’A=B’QC (ALA) por lo tanto F’A=QC=S
Luego AQ es una de la s alturas iguales del triángulo isósceles del triángulo B’ABes decir BF=AQ=R
Finalmente los triángulos PNF’ y BFG son congruentes (ALA) entonces PN=FG=n
Por ultimo en el triángulo rectángulo C’NC (AH es base media)
![]() es decir.
es decir. ![]()
Prof.: William Rodríguez chamache