Problema 176

Sea un triángulo  rectángulo  y no isósceles.

Sea  la altura sobre la hipotenusa.

Sean B’, C’ los simétricos de B i C respecte l’eix .

Construimos los triángulos  y  siendo A’ sobre la recta  tal que  sea paralelo a .

Sean  y  las alturas de los vértices B i C’ de los triángulos , .

Por F y F’ trazamos  y  perpendiculares de F y F’ sobre .

Probar que  es media aritmética de los segmentos  y

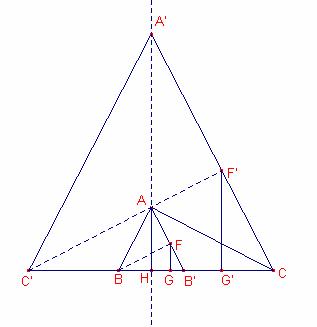
Solución de Ricard Peiró i Estruch, profesor de Matemáticas del IES 1 de Xest (València)

:

Sea

Por el teorema de la altura de un triángulo rectángulo :

    

Aplicando los teoremas de los catetos al triángulo rectángulo :

, 

Aplicando razones trigonométricas al triángulo :

Los triángulos  son semejantes.

La razón de semejanza es

Entonces,

Aplicando razones trigonométricas al triángulo rectángulo :

Aplicando el teorema de Pitágoras al triángulo rectángulo :

Calculemos el área del triángulo :

,  

Igualando las áreas y simplificando: