Problema 178.

Tenemos un triángulo ABC con D sobre CB, tal que AC=CD, y <CAB - < ABC =30º.

Hallar la medida del ángulo BAD.

Goldin G.A. y McClintock, C.E. (1984): Task variables in mathematical problem solving.

Franklin Intitute Press. p. 232

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

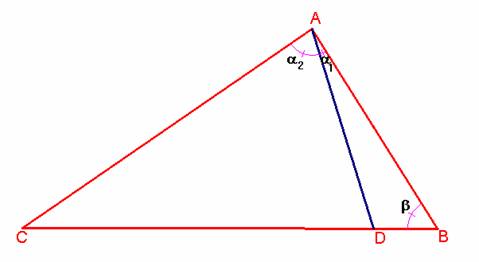
Si llamamos a=<CAB,  a₁ =<DAB , a₂ =<DAC y b=<ABC, tenemos que: a₁ + a₂ = a

Como el triángulo ACD es isósceles, con ángulos iguales <CAD = <ADC = a₂, se tendrá que: <ACD = 180º -2a₂ y, como consecuencia b= a₂ - a₁.

Imponiendo ahora la condición  dada:
<CAB - < ABC = a - b = 30º
se obtiene la igualdad:

a - b = (a₁ + a₂ ) - (a₂ - a₁ ) = 2a₁ = 30º
Por tanto:         a₁ = 15º