Sea el triángulo sea D sobre el lado tal que y

Calcular la medida del ángulo

Goldin G.A. y McClintock, C.E. (1984): Task variables in mathematical problem solving.

Franklin Intitute Press. p. 232

Solución de Ricard Peiró i Estruch, profesor de Matemáticas del IES 1 de Xest (Valencia)

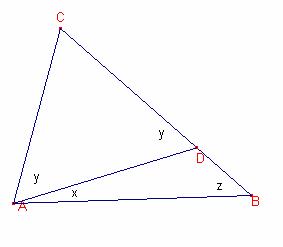
Solución:

Sea , ,

Como el triángulo es isósceles, entonces, .

Aplicando la propiedad de la suma de los angulos de un triángulo es un ángulo llano al triángulo

(1)

Por hipótesis (2)

Consideremos el sistema formado por (1) (2)

Sumando las dos ecuaciones:

Entonces,