Problema 179

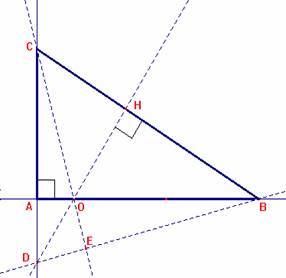
Sea ABC un triángulo rectángulo en A. Por un punto O del cateto AB trazamos la perpendicular OH a la hipotenusa BC. Sea D el punto de intersección de la recta OH con la recta AC. Tracemos BD. Sea E el punto de intersección de la recta BD con la CO.
Hallar el lugar geométrico de E cuando O recorre AB.

André, M. Ph. (1920). Éléments de GÉOMÉTRIE Conformes aux programmes de baccalauréats (1re partie) de l'enseignement secondaire classique et de l'enseignement secondaire moderne. Contenant plus de mille problémés résolus et a resoudre.(Treinte-quatriéme edition). Paris, Librairie classique de FE André Guédon.
E. Andre Fils Succeseur, 6 rue Casimir-Delavigne (près l'Odeon). (p. 82)

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.

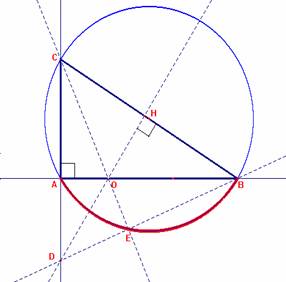
            Analizada la situación dada, observamos que el triángulo BCD tiene como ortocentro al propio punto O. Por tanto, el punto E será el pie de la perpendicular trazada por C al lado BD. De esta forma, E pertenecerá al arco de la circunferencia de diámetro BC comprendido entre los puntos A y B como los dos puntos límite del lugar geométrico deseado.