Solución del problema 179. José Montes Valderrama. Profesor del Centro Publico de Educación de Adultos “Triana”.

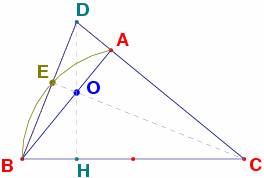
Sea ABC un triángulo rectángulo en A.

Por un punto O del cateto AB tracemos la

perpendicular OH a la hipotenusa BC.

Sea D el punto de intersección de la recta OH con la recta AC.

Tracemos BD. Sea E el punto de intersección de la recta BD con la CO.

Hallar el lugar geométrico de E cuando O recorre AB.

André, M. Ph. (1920). Éléments de GÉOMÉTRIE Conformes aux programmes de baccalauréats (1re partie)

de l'enseignement secondaire classique et de l'enseignement secondaire moderne. Contenant plus de mille

problémés résolus et a resoudre.(Treinte-quatriéme edition). Paris, Librairie classique de FE André Guédon.

E. Andre Fils Succeseur, 6 rue Casimir-Delavigne (près l'Odeon). (p. 82)

Consideremos previamente una sencilla pero no menos interesante propiedad.

Sea el triángulo PQR y k una circunferencia cuyo diámetro sea el lado QR.

Si Q´y R´ son los pies de las alturas de Q y R entonces pertenecen a la circunferencia k.

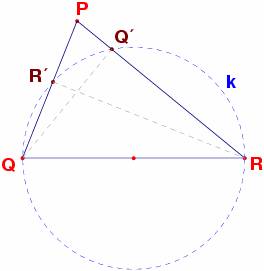
Es evidente que los triángulos QRR´y QRQ´son rectángulos por la construcción de las alturas y por ello están inscritos en la semicircunferencia que el diámetro (lado) QR determina en k.

En el problema, el triángulo DBC tiene por alturas BA por ser ABC rectángulo y OH por construcción. En consecuencia, O es el ortocentro de DBC y además CE, al pasar por O, es necesariamente su tercera altura.

Así, por la propiedad anterior, en el triángulo DBC, siendo los pies de las alturas de C y B los puntos E y A, se verifica su pertenencia a la circunferencia cuyo diámetro es el lado BC.

En conclusión, el lugar geométrico de E cuando O recorre el cateto AB es el arco AB de la circunferencia que circunscribe al triángulo ABC.