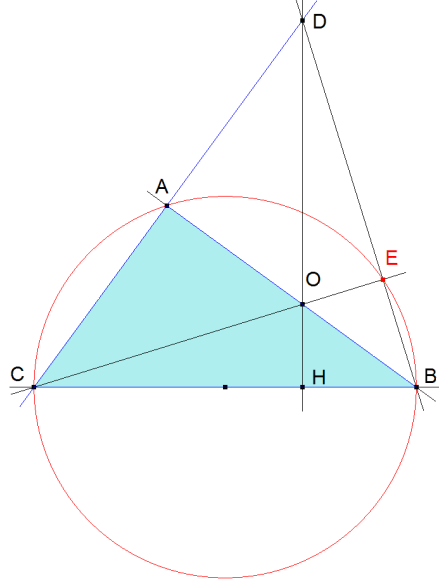
Problema 179

Sea ABC un triángulo rectángulo en A.

Por un punto O del cateto AB tracemos la perpendicular OH a la hipotenusa BC.

Sea D el punto de intersección de la recta OH con la recta AC.

Tracemos BD. Sea E el punto de intersección de la recta BD con la CO.

Hallar el lugar geométrico de E cuando O recorre AB.

André, M. Ph. (1920). Éléments de GÉOMÉTRIE Conformes aux programmes de baccalauréats (1re partie) de l'enseignement secondaire classique et de l'enseignement secondaire moderne. Contenant plus de mille problémés résolus et a resoudre.(Treinte-quatriéme edition). Paris, Librairie classique de FE André Guédon. E. Andre Fils Succeseur, 6 rue Casimir-Delavigne (près l'Odeon). (p. 82)

Solución de José Mará Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona)

Fijémonos en el triángulo BCD. Por ser ABC rectángulo en A, AB es una altura de BCD. Por ser OH perpendicular a BC es otra altura de BCD. O es entonces el ortocentro de BCD y por tanto, CE es la tercera altura de BCD. < CEB es recto y sus catetos pasan por B y C. EL LUGAR DE ES EL CIRCULO DE DIAMETRO BC (circunscrito ABC).