Problema 179

En un el triángulo rectángulo .

Por el punto O del cateto tracemos la perpendicular a la hipotenusa .

Sea D la intersección de la recta OH y la recta AC.

Sea E la intersección de las rectas DB y OC.

Determinar el lugar geométrico del punto E al variar O sobre el cateto .

André, M. Ph. (1920). Éléments de GÉOMÉTRIE Conformes aux programmes de baccalauréats (1re partie)

de l'enseignement secondaire classique et de l'enseignement secondaire moderne. Contenant plus de mille

problémés résolus et a resoudre.(Treinte-quatriéme edition). Paris, Librairie classique de FE André Guédon.

E. Andre Fils Succeseur, 6 rue Casimir-Delavigne (près l'Odeon). (p. 82)

Solución de Ricard Peiró i Estruch Profesor de Matemáticas del IES 1 de Xest (València):

Propiedad de un triángulo rectángulo:

a) La mediana de un triángulo rectángulo trazada a la hipotenusa es igual a la mitad de la hipotenusa.

b) Si un triángulo una de las medianas mide la mitad del lado sobre la que está trazada, el triángulo es rectángulo.

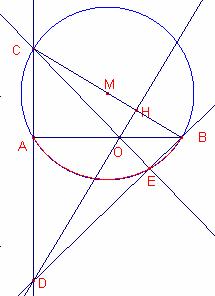
Sean , , .

Demostremos que .

Consideremos el rectángulo ,

Consideremos el rectángulo ,

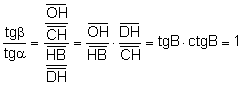
Entonces, , por tanto,

Los triángulos , son semejantes, por tanto es rectángulo.

Siga M el punto medio de la hipotenusa .

Por la propiedad de la mediana de un triángulo rectángulo:

, El segmento es siempre constante.

Entonces el lugar geométrico del punto E al variar O sobre el cateto es el arco de circunferencia de centro M y radio .