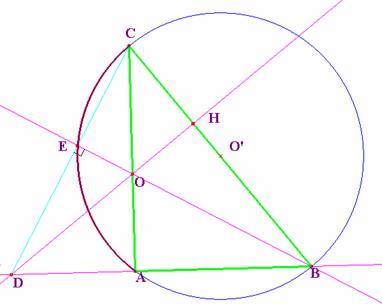
Problema 179.- Sea ABC un triángulo rectángulo en A. Por un punto O del cateto AB tracemos la perpendicular OH a la hipotenusa BC. Sea D el punto de intersección de la recta OH con la recta AC. Tracemos BD. Sea E el punto de intersección de la recta BD con la CO. Hallar el lugar geométrico de E cuando O recorre AB.

André, M. Ph. (1920). Éléments de GÉOMÉTRIE Conformes aux programmes de baccalauréats (1^re partie) de l'enseignement secondaire classique et de l'enseignement secondaire moderne. Contenant plus de mille problémés résolus et a resoudre.(Treinte-quatriéme edition). Paris, Librairie classique de FE André Guédon. E. Andre Fils Succeseur, 6 rue Casimir-Delavigne (près l'Odeon). (p. 82)

SoluciónSolución de Saturnino Campo Ruiz, profesor de Matemáticas del I.E.S. Fray Luis de León (Salamanca).-

La recta DH por construcción, es perpendicular a BC; también AC es perpendicular a AB (son dos catetos del mismo triángulo), de ahí que el punto de encuentro de ambas, O, sea el ortocentro del triángulo BCD, y, en consecuencia, la recta BE sea perpendicular a CD.

De todo esto se deduce que el punto E pertenece al arco capaz del segmento BC y amplitud 90º, es decir es el arco AEC de diámetro BC y centro O’ (punto medio de BC).