Problema 179
Sea ABC un triángulo rectángulo en A.
Por un punto O del cateto AB tracemos la
perpendicular OH a la hipotenusa BC.
Sea D el punto de intersección de la recta OH con la recta AC.
Tracemos BD. Sea E el punto de intersección de la recta BD con la CO.
Hallar el lugar geométrico de E cuando O recorre AB.
André, M. Ph. (1920). Éléments de GÉOMÉTRIE Conformes aux programmes de baccalauréats (1re partie)
de l'enseignement secondaire classique et de l'enseignement secondaire moderne. Contenant plus de mille
problémés résolus et a resoudre.(Treinte-quatriéme edition). Paris, Librairie classique de FE André Guédon.
E. Andre Fils Succeseur, 6 rue Casimir-Delavigne (près l'Odeon). (p. 82)
Solución de William Rodríguez Chamache. profesor de geometria de la "Academia integral class" Trujillo- Perú
Consideraciones iniciales
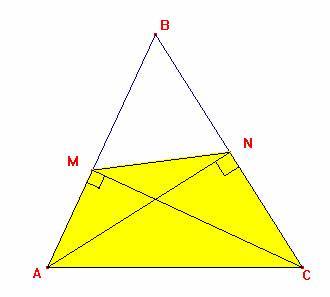
1ro) En el gráfico mostrado el cuadrilátero AMNC es inscriptible (cuadrilátero que por sus vértices pasa una circunferencia) luego AC es el diámetro de una sola circunferencia luego los punto M y N pertenecen a dicha circunferencia
Propiedad: todo punto que pertenece a una circunferencia al ser unida a los extremos de cualquier diámetro de dicha circunferencia forman ángulo de 90º
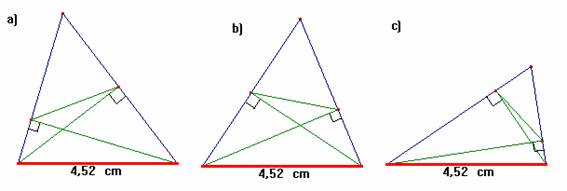
En los tres casos los cuadriláteros son inscriptibles y tiene una misma base que para cada caso es un diámetro finalmente todos los puntos de los cuadriláteros pertenecen a una misma circunferencia
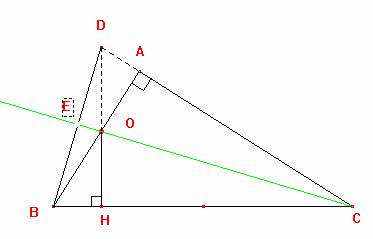
Solución:
En el gráfico observamos que O es el ortocentro del triángulo BDC finalmente el ángulo BEO es 90º
luego observamos que el cuadrilátero BEAC es inscriptible luego por sus vértices pasa una circunferencia
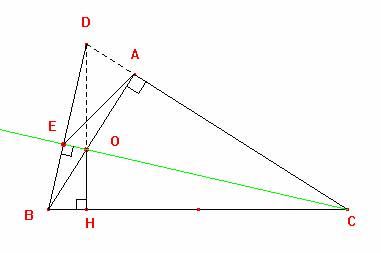
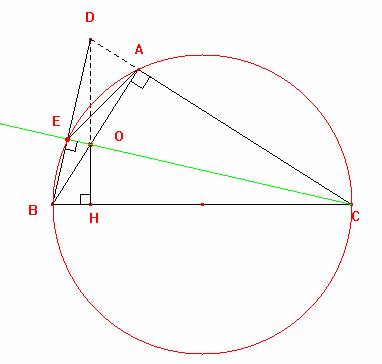
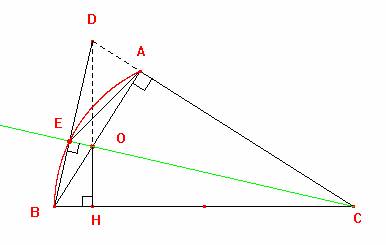
Luego como el punto O solo se mueve a lo largo del segmento AB entonces el punto E se desplazara solo por el arco AEB finalmente el lugar geométrico que describe será un arco de la circunferencia subtendida por la cuerda AB.
Prof.: W.R.Chamache