Problema 180

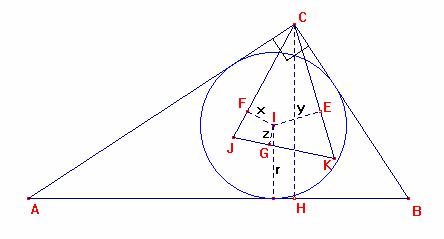
El triángulo ABC es recto en C, CH es altura, I, J y K son incentros de los triángulos ABC, AHC y BHC. Si x = IF, y = IE, z = IG son las distancias desde I hacia JC, KC y JK, respectivamente. Demostrar que: , donde r es inradio de ABC.
Ver figura:

Salazar, J. C. (2004): Comunicación personal.

Solución de F. Damián Aranda Ballesteros, profesor del IES Blas Infante de Córdoba.
            Analizada la situación dada, observamos que I es el ortocentro del triángulo CJK. Esto es así ya que, al ser K el incentro del triángulo BHC, entonces <KCB=A/2. Así el ángulo <ACK= 90º-A/2. Por tanto, las rectas AJ (=JI) y CK se cortan perpendicularmente. Este punto de corte no es otro que el punto E.

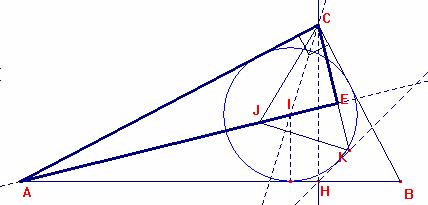De igual manera, se probaría que la recta BK (=KI) corta perpendicularmente al lado CJ en el punto F.

Luego I es, en efecto, el ortocentro del triángulo CJK y así la recta CI cortará perpendicularmente al lado JK en el punto G.

Fijaremos a continuación una serie de resultados sobre las medidas de algunos ángulos notables que resultan en la figura dada.

Así ahora es fácil averiguar que:

<ACJ = B/2; <AJC = 135º; <FJI  = 45º; FJ  = x

<BCK= A/2; <BKC= 135º; <EKI= 45º; EK= y

Deducimos que <JIK= 135º ya que <JIC= 135º-A/2 y <BIC=135º-B/2.
Por tanto, <JIK= 360º- (<JIK + <JIC)= 135º

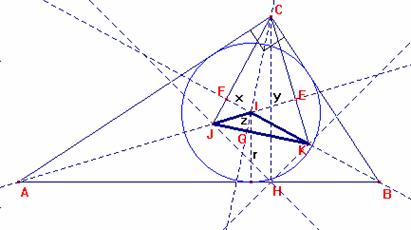Nos fijaremos ahora en el triángulo JIK.

De este triángulo, conocemos sus lados ,  

y el ángulo que determinan entre sí,  <JIK= 135º.
También conocemos una de sus alturas,
IG = z, respecto del lado JK.

Así, relacionamos estos datos de la siguiente manera:

            [IJK]=

            [IJK]=            
De donde, . Si probamos que, en efecto, , estaría ya todo probado.

Para hacer esto último, consideramos los siguientes triángulos rectángulos IFC y JFK

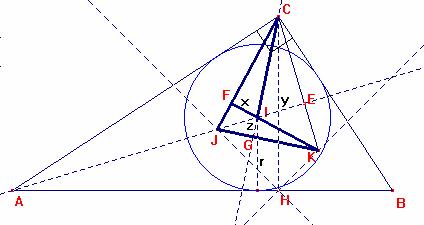
En el triángulo IFC, tenemos que IF = x y su ángulo opuesto es , mientras que en triángulo JFK, JF = x y su ángulo opuesto es .

(= Para ver esto último, téngase en cuenta que el cuadrilátero FIGJ es cíclico y así,
<FIG + <FJG= 180º. Como <FIG + <FIC= 180º, entonces <FJG= <FIC).

Por tanto, ambos triángulos son iguales. En concreto, IC = JK, pero , luego .
Por tanto, en efecto, y así queda probada la relación:  , c.q.d.