180

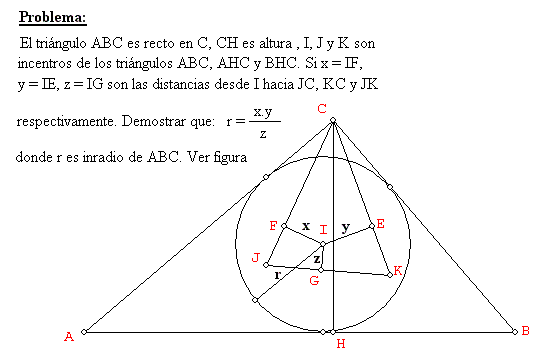
Solución de Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz). Problema 180:

Ver Figura siguiente.

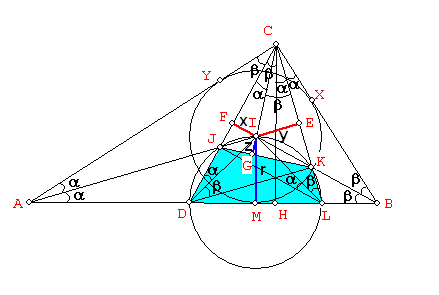
Al trazar las bisectrices AJ, CJ, BK, CK tenemos que CJ y CK cortan a AB en D y L respectivamente. Luego se cumple que:

<JAC = <JAB = <HCK = <KCB = a y <JCA = <JCH = <KBA = <KBC = b

También: <ICA = <ICB =45º = a + b, entonces:

<ICA = <JCA + <JCI = a + b = <ICB = <ICK + <KCB, por lo tanto:

<ICA = b + <JCI = a + b, entonces: <JCI = a

<ICB = <ICK + a = a + b, entonces: <ICK = b.

Además el triángulo CAL es isósceles porque: <ALC = <LCB + <B = a + 2 b = <LCA

También el triángulo DBC es isósceles donde: <BDC = < DCB = b + 2 a.

Por expuesto tenemos que AJ y son BK son bisectriz y mediatriz en los triángulos isósceles CAL y DBC, y se cortan en I, incentro del triángulo ABC respectivamente, entonces las distancias IE, IF desde I hacia CK y CJ son segmentos contenidos en las rectas AJ y BK respectivamente, donde:

<ILC = <ICL = b y <IDC = <ICD = a, por lo tanto el cuadrilátero ADIC es inscriptible, ya que <CDI = <IAC = a, igualmente el cuadrilátero BLIC también es inscriptible, porque <ILC = <IBC = b. Luego se cumple que:

<LIB = <LCB = a y < DIA = <DCA = b

Por otro lado:

<IKC = <KCB + <KBC = a + b = 45º = <IDL

<IJC = <JAC + <JCA = a + b = 45º = <ILD.

Es decir que los puntos D, J, I, K, L están en una circunferencia de diámetro DL = 2r, porque <DIL = 90º donde IM = r es perpendicular a DL y DI = IL.

De todo lo indicado, tomando como referencia al cuadrilátero DJKL, aplicamos el teorema de Pappus, para las distancias IF e IE hacia los lados DJ y KL respectivamente con las distancias IG e IM hacia los lados JK e IL respectivamente, entonces:

IF.IE = IG.IM

x.y = r.z

r = x.y/z QED.

Juan Carlos Salazar

caisersal@yahoo.com