Propuesto por Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz).
Problema 180.
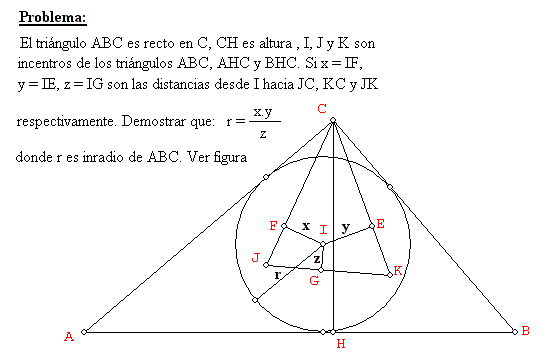
Salazar, J.C. (2004): Comunicación personal.
Solución de William Rodríguez Chamache, profesor de geometria de la "Academia integral class" Trujillo- Perú :
Consideraciones iniciales
Al prolongar las bisectrices CJ y CK cortan a la hipotenusa AB en los puntos N y M entonces los triángulo determinados son isósceles es decir CB =BN y AC =AM
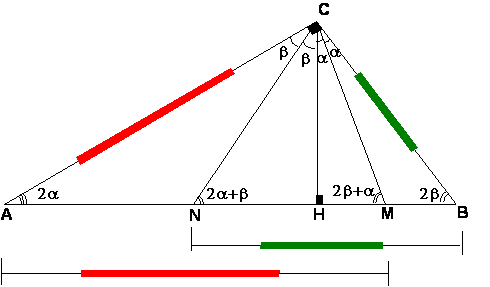
Luego en este gráfico que AT=AP=m entonces PM=r, (ver nota del editor)lo mismo con los segmentos EB=BP=n entonces NP=r, finalmente el segmento MN=2r
Ahora las bisectrices de los ángulo A y B pasan por el incentro I del triángulo ABC y son perpendiculares a los segmentos CM y CN respectivamente (por ser triángulo isósceles CAM y CBN). Además no olvidar que el ángulo MCN =α+β = 45
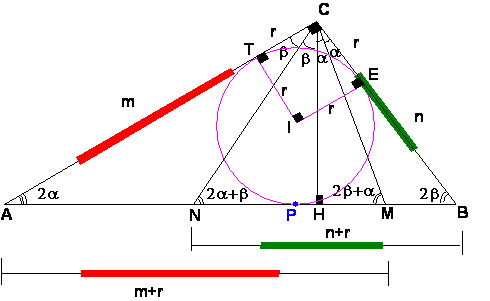
Ahora como K es un punto de la mediatriz del segmento CN se cumple que CK=NK luego el triángulo NKC es rectángulo isósceles de ángulo recto en K
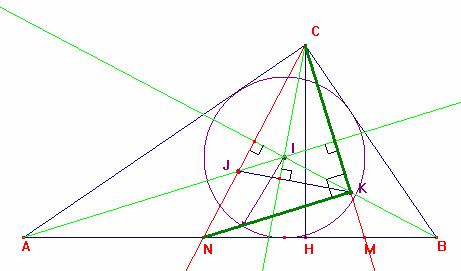
La misma operación en el triángulo isósceles CAM J es un punto de la mediatriz del segmento CM luego los segmentos JC=JM y el triángulo CJM es rectángulo en J=90º
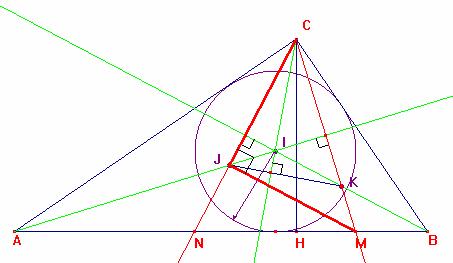
Entonces podemos observar que el cuadrilátero NJKM es inscriptible luego los puntos N, J, K y M están sobre la circunferencia de diámetro MN = 2r, pero el cuadrilátero JIKM es trapecio isósceles (los ángulos KMJ=IJM=45º además JM//IK) finalmente el trapecio isósceles es inscriptible los puntos J, I, K y M están sobre una circunferencia finalmente los puntos N, J, I, K, y M son ciclicos a una circunferencia de diámetro MN=2r
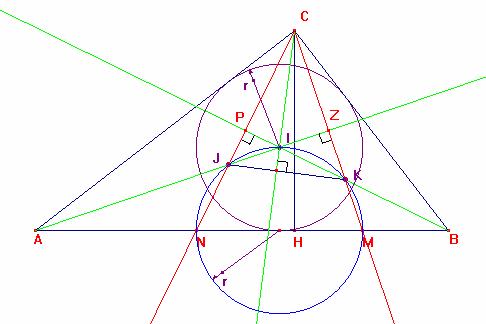
Del gráfico JI=![]() y KI=
y KI=![]()
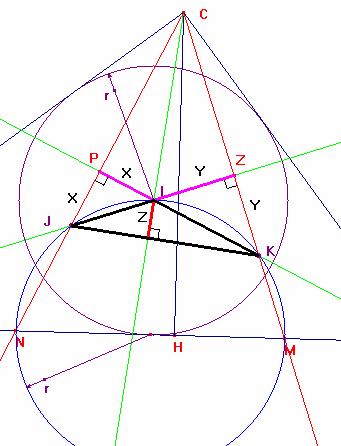
Finalmente en el triángulo JIK se cumple que:
![]() ................... resolviendo:
................... resolviendo: ![]()
Prof.: William Rodríguez Chamache