Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid

Problema 181

El lado AB en el triángulo ABC es mayor que AC, y D es el punto medio de BC. Desde C dibujamos dos perpendiculares a la bisectrices interior y exterior en el ángulo A encontrando a aquellas en F y G respectivamente.

Probar que :

(i) DF = (1/2)(AB-AC);

(ii) DG = (1/2)(AB+AC)

Aref, M.N., Wernick, W. (1968): Problems and Solutions in Euclidean Geometry, Dover, New York, p.9-10

Solución de José Mará Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona)

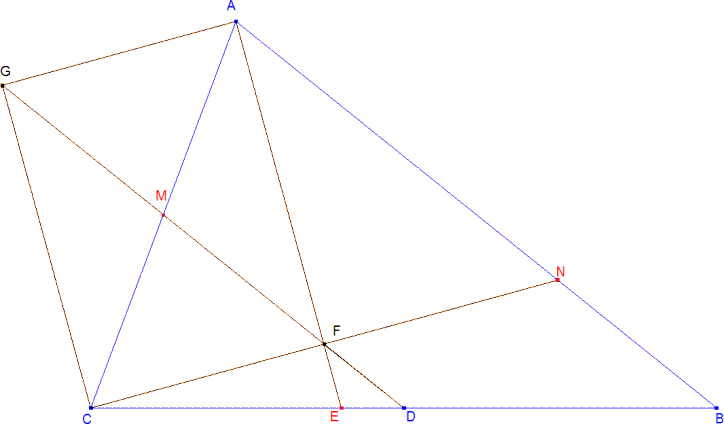
LAS RECTAS AB Y GF SON PARALELAS, GF PASA POR D Y CMD ES HOMOTETICO DE CAB

las bisectrices AE y AG son ortogonales y ello nos indica que F y G son vértices opuestos del paralelogramo AFCG y por lo tanto M es el punto medio de AC, además AM = FM y por lo tanto AMF es isósceles y así ∠AFM es A/2 y su opuesto por el vértice ∠EFD también es A/2; ahora bien ∠EAB es A/2; así deducimos que GF y AB son paralelas.

Como M es punto medio de AC y GF es paralela a AB entonces GF pasa por D.

Como MD pasa por los puntos medios de AC y BC; entre CMD y CAB, el centro de homotecia es C y la razón ½.

EL TRIANGULO ANC ES ISOSCELES

Los ángulos ∠CAE y ∠EAB son iguales a A/2 y los ángulos ∠AFE y ∠AFN son iguales a π/2; entonces los ángulos ∠ACF y ∠ANF son iguales entre sí y por tanto ANC es isósceles y AN = AC.

CONCLUSION

(i) AN = AC y por la homotecia DF = BN/2 = (AB-AN)/2 = (AB-AC)/2.

(ii) AN = AC y por paralelas entre paralelas FG = AN. DG = DF+FG = DF + AC = (AB-AC)/2 + AC = (AB+AC)/2.