Propuesto por Juan Bosco Romero Márquez, profesor colaborador de la Universidad de Valladolid
Problema 181
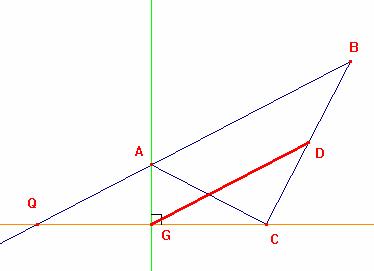
1.10 El lado AB en el triángulo ABC es mayor que AC, y D es el punto
medio de BC. Desde C dibujamos dos perpendiculares a la bisectrices
interior y exterior en el ángulo A encontrando a aquellas en F y G
respectivamente.
Probar que :
(i) DF =(1/2)(AB-AC);
(ii) DG =(1/2)(AB+AC)
Aref, M.N., Wernick, W. (1968): Problems and Solutions in Euclidean Geometry,
Solución:
1er caso
Prolongamos la perpendicular CF hasta cortar al segmento AB en T luego el triángulo CAT es isósceles (AF es altura y bisectriz también será mediana y mediatriz) por lo tanto AC = AT Ahora en el triángulo BCT. FD es base media luego su medida será la mitad de TB finalmente: FD = ![]()

2do caso
se prolonga la perpendicular CG hasta cortar a la prolongación de BA en Q luego le triángulo CAQ es isósceles (caso anterior) luego AC = AQ y como G y D son puntos medios GD es base media luego su medida será la mitad del segmento BQ finalmente FD = ![]()