|
|||
Propuesto por Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca Problema 182 - EL TEOREMA DE LOS POLÍGONOS CERRADOS DE PONCELET. Se tienen dos circunferencias una k dentro de otra K. Supongamos que desde un punto A de K (la exterior) sucede lo siguiente: Trazamos por A una tangente a k que vuelve a cortar a K en B; por B trazamos la otra tangente a k, que vuelve a cortar a K en C; por C trazamos la otra tangente a k, que resulta que vuelve a cortar a K en A (es decir, se cierra la sucesión de tres tangentes). Entonces eso mismo pasa (es decir el triángulo también se cierra) cuando hacemos la misma operación partiendo de cualquier otro punto A* de K. ¡Demostrarlo! Guzmán, M. de (2002): La experiencia de descubrir en Geometría. Nivola Libros pág. 102. En el enunciado anterior puede sustituirse la palabra circunferencia(s) por cónica(s) y el enunciado subsiste. Solución de José Mará Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona) |
|||
|
|||
0. |
INTRODUCCION |
||
|
|||
|
¡Qué hermoso problema nos ha propuesto SATURNINO CAMPO! Este problema es un caso particular de un teorema mucho más potente que asegura el mismo resultado para cónicas y polígonos de n lados (n ≥ 3). No está de más, echar un vistazo a la página del admirado PROFESOR GUZMAN sobre este tema: http://nonio.mat.uc.pt/PENSAS_EN02/experdescgeomet/11poncelet/11poncelet.html Como sugiere SATURNINO, me dedicaré al caso del triángulo y cónicas en general. Más adelante, con tiempo, presentaré una generalización al polígono de n lados parecida a la del profesor SANTALO en su libro de geometría proyectiva. Existe una infinidad de referencias bibliográficas respecto a este tema. Aunque la intención es usar los resultados más sencillos, podemos ver el documento sobre cónicas proyectivas del problema 137 de las páginas de RICARDO BARROSO: La demostración que pretendo se basará en: |
|||
- - - - - - |
la definición clásica de las cónicas,
una propiedad de las cónicas y sus tangentes, base de toda la teoría de estas curvas que demostraremos apoyándonos en el círculo y sus propiedades,
veremos a continuación propiedades relativas a los puntos de la cónica
y propiedades relativas a las tangentes,
de lo anterior, podremos deducir un teorema (GRAN TEOREMA DE PONCELET)
y como corolario el resultado buscado. |
||
|
La originalidad en un tema como éste es difícil; creo que lo que esta presentación aporta es un camino simple y detallado para llegar al resultado. Se me ha ocurrido porque conocía el teorema de Poncelet y como lo que pretendo es simplicidad, no usaré conceptos de dualidad o correlación (polos y polares).
La demostración supone conocido: |
|||
- - - - - - |
que es un cono y algo de ángulos inscritos en círculos,
que es un haz de rectas
que es la razón doble (de cuatro puntos y de cuatro rectas de un haz) y sus propiedades
que es una tangente
que es una proyección
y que es una homografía . |
||
|
|||
1. |
DEFINICION CLASICA DE CONICA |
||
|
|||
|
Se denomina SECCIONES CONICAS o simplemente CONICAS las curvas por las que un cono de base circular puede ser cortado por planos cualesquiera.
Las imágenes son de http://www.math2.org/math/algebra/es-conics.htm |
|||
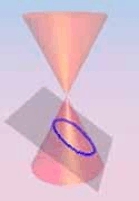 ELIPSE Si el plano cualquiera corta todas las aristas del cono, lo corta en una curva cerrada. |
 PARABOLA Si el plano es paralelo a algún plano tangente del cono lo corta en una curva con una rama infinita. |
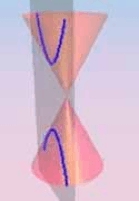 HIPERBOLA. Si el plano es paralelo a dos aristas del cono, lo corta en una curva con dos ramas infinitas. |
|
|
|||
2. |
PROPIEDAD BASICA DE LAS CONICAS |
||
|
|||
|
Teorema 2 Sean las tangentes por cuatro puntos de una cónica y sean otras cuatro rectas concurrentes en un punto de la curva. La razón doble de estas cuatro rectas será igual a la de los cuatro puntos de encuentro de las cuatro tangentes con una quinta tangente cualquiera.
Demostración Como las proyecciones (centro de proyección el vértice del cono y rayos las aristas) conservan la razón doble de cuatro puntos y de cuatro rectas, bastará demostrar este teorema para el círculo que forma la base del cono sobre el que se considere la cónica. Sobre el círculo, la prueba no sólo es más sencilla sino que resulta casi evidente. |
|||
|
|||
|
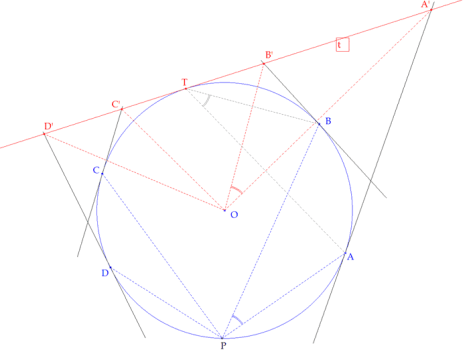
Sean A, B, C, D cuatro puntos del círculo; AA’, BB’, CC’, DD’ las tangentes en estos puntos y A’, B’, C’, D’ los puntos de encuentro de estas tangentes con t la tangente al círculo por un quinto punto T.
Sea P un punto cualquiera del círculo. El haz de rectas PA, PB, PC, PD tiene la misma razón doble que los cuatro punto alineados A’, B’, C’, D’: |
|||
|
El ángulo ∠APB es igual al ángulo ∠ATB; y éste a su vez al ángulo ∠A’OB’ por ser ángulos con los lados perpendiculares. Entonces Las rectas PA, PB, PC, PD forman entre sí los mism ángulos que las rectas OA’, OB’, OC’, OD’ y por tanto los dos haces tienen la misma razón doble. Como OA’, OB’, OC’, OD’ tiene la misma razón doble que A’, B’, C’, D’, obtenemos el resultado buscado. |
|||
|
|||
3. |
PROPIEDAD FUNDAMENTAL RELATIVA A LOS PUNTOS DE LAS CONICAS |
||
|
|||
|
Teorema 3 Si de cuatro puntos de una cónica trazamos rectas que concurren en un quinto punto de la cónica; la razón doble de esas cuatro rectas tiene un valor constante independiente del quinto punto.
Demostración Poco hay que demostrar atendiendo a lo anterior (teorema 2), ya que las cuatro rectas PA, PB, PC, PD tienen la razón doble igual a la de los cuatro puntos de intersección de las cuatro tangentes por A, B, C, D con una quinta tangente y eso para cualquier punto P de la cónica.
Otra forma de enunciado. Teorema 3.1 Según lo visto, dados dos puntos fijos de la cónica P y P’ y uniéndolos a otros cuatro puntos de la cónica tendremos dos haces de cuatro rectas con la misma razón doble y por lo tanto el teorema 3 se puede enunciar como sigue:
Si desde dos puntos fijos de una cónica se trazan sendas rectas variables que se cortan siempre sobre la curva, entonces esas rectas forman dos haces homográficos.
Teorema 3.2 recíproco La curva, lugar geométrico de los puntos de intersección de las rectas homólogas de dos haces homográficos, es una cónica que pasa por los vértices de los dos haces.
Esto equivale a decir que podemos hacer pasar por la curva un cono de base circular. (No demuestro el teorema recíproco porque en este ejercicio no nos es necesario). |
|||
|
|
|||
|
|||
4. |
PROPIEDAD FUNDAMENTAL RELATIVA A LAS TANGENTES DE LAS CONICAS |
||
|
|||
|
Teorema 4 Cuatro tangentes fijas de una conica son cortadas por una quinta tangente cualquiera en cuatro puntos cuya razón doble es constante.
Demostración Demostración simple, ya que como hemos visto con la propiedad básica (teorema 2), esta razón doble es la de cuatro rectas por los puntos de contacto y que concurren sobre un quinto punto fijo y arbitrario de la cónica.
Otro forma de enunciado. Teorema 4.1 Los puntos de intersección de una tangente móvil con dos tangentes fijas son homográficos.
Teorema 4.2 recíproco La curva envolvente, de las rectas que unen los puntos homólogos en una homografía de dos rectas, es una cónica tangente a esas dos rectas.
Demostración (M. Chasles) Este enunciado equivale a decir que podemos hacer pasar por la curva un cono de base circular. |
|||
|
|||
|
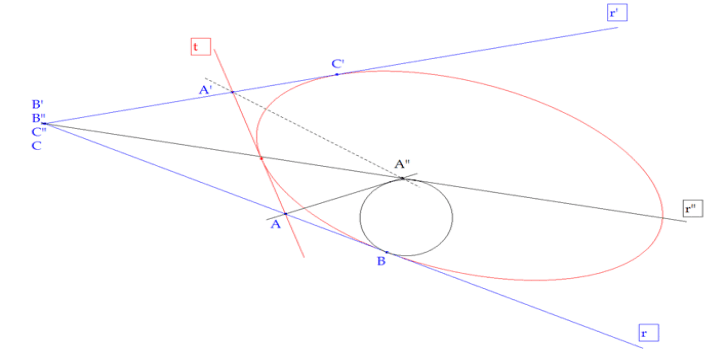
Sea dos rectas r y r’ y una homografía entre ellas definida por A→A’, B→B’, C→C’ con A, B, C sobre r y A’, B’, C’ sobre r’. (el punto r∩r’ como punto de r es C y como punto de r’ es B’)
Sea t la recta que une dos puntos homólogos cualesquiera (en la figura AA’), Observando la figura, vemos que la curva envolvente será tangente a BB’ y por tanto tangente a r en B y la envolvente también será tangente a CC’ y por tanto tangente a r’ en C’.
Trazamos por B un círculo tangente a r y llevamos tangentes a este círculo desde todos los puntos de r (en la figura desde A). Sea r” la tangente al círculo desde r∩r’; entonces todas las tangentes desde un punto A de r encontrarán a r” en un punto A”. Por el teorema directo 4.1 A y A” son homográficos ; pero A y A’ también son homográficos, entonces A” y A’ son también homográficos, pues dos rectas homográficas a una tercera son homográficas entre sí.
Basta observar la figura para ver que r∩r’=B’=B” es un punto común de esta homografía entre r’ y r”. Podemos pues decir que esa última homografía es una PROYECCÍON pues una homografía entre rectas es una proyección si y sólo si el punto de intersección de las rectas se transforma en sí mismo. (Igual ocurriría si hiciéramos girar el plano del círculo y la tangente r” en torno de la recta r; es decir, para cada posición de ese plano las rectas A’A” concurren en un mismo punto del espacio).
Entonces todas las rectas del tipo A’A” pasarán siempre por un punto fijo Ω (centro de proyección). Tomando ese centro de proyección Ω podremos considerar a cada recta AA’ como la proyección de las rectas AA” y por lo tanto, la envolvente de las rectas AA’ será la proyección de la envolvente de las rectas AA”; pero esa última envolvente es un círculo y por tanto la curva buscada está sobre un cono de base circular. |
|||
|
|||
|
|
|||
|
|
||
5. |
GRAN TEOREMA DE PONCELET |
||
|
|||
|
Teorema 5 Cuando dos triángulos están inscritos a una cónica, los seis lados son tangentes a otra cónica. |
|||
|
|||
|
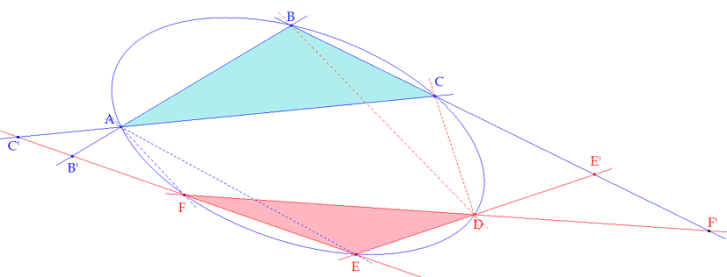
Demostración Sean ABC y DEF los dos triángulos inscritos en la cónica Γ. Los dos haces de rectas A*=(AB, AC, AE, AF) y B*=(DB, DC, DE, DF) tienen la misma razón doble (teorema 3). AB y AC cortan a FE respectivamente en B’ y C’.DE y DF cortan a BC respectivamente en E’ y F’. Las intersecciones del haz A* con EF son B’, C’ E, F. Las intersecciones del haz B* con BC son B, C, E’, F’. Se produce así la igualdad de razones dobles (B’, C’ E, F) = (B, C, E’, F’); entonces hemos definido una homografía entre las rectas BC y EF.
Al haber definido la homografía anterior, hemos visto (teorema 4.2) que las rectas que unen puntos homólogos BB’, CC’, EE’, FF’ y las rectas dadas BC y EF son tangentes a una misma cónica Γ’.
Teorema 5.1 recíproco De una manera análoga a la anterior podríamos demostrar de forma recíproca:
Cuando dos triángulos son circunscritos a una cónica, sus seis vértices están sobre otra cónica. |
|||
|
|||
6. |
TEOREMA DE LOS POLIGONOS CERRADOS DE PONCELET (CASO DEL TRIANGULO) |
||
|
|||
|
|
|||
|
Teorema 6
Como corolario del teorema anterior (teorema 5) o su recíproco:
Cuando un triángulo ABC está inscrito a una cónica Γ y circunscrito a una cónica Γ’, se puede construir una infinidad de triángulos inscritos a Γ y circunscritos a Γ’.
Si de un punto A’ de Γ se trazan dos tangentes a Γ’ interceptarán en Γ una cuerda B’C’ que forma con esas tangentes el triángulo A’B’C’. Los dos triángulos ABC y A’B’C’ tienen sus seis lados tangentes a una misma cónica (teorema 5). Esta cónica sólo puede ser Γ’, tangente a los tres lados del primer triángulo y a dos lados del segundo. |
|||
|
|||
7. |
NOTAS |
||
|
|||
|
Nota 1 Hemos empezado viendo la definición clásica de la sección cónica, por ser el cono de base circular lo que ayuda a concluir la demostración del teorema 4.2 (recíproco del teorema 4 y 4.1). Si hubiéramos tenido necesidad de demostrar el teorema 3.2 (recíproco del 3 y 3.1) hubiéramos también usado el cono.
Nota 2 La demostración del la propiedad básica de las cónicas (teorema 2) ,a parte de la razón doble, sólo usa la igualdad de ángulos inscritos a un círculo cuando sus lados comprenden la misma cuerda.
Nota 3 Las demostraciones de los teoremas directos fundamentales (3, 3.1, 4 y 4.1) son simples conclusiones del teorema 2.
Nota 4 Más complicada es la demostración de los recíprocos (4.2), en especial para la identificación de la proyección entre dos rectas y la visión del punto en el espacio no es directa y simple. Chasles, por ejemplo, tomó la idea del círculo de un alumno suyo.
Este teorema se encuentra demostrado en multitud de fuentes. Por citar sólo dos: |
|||
a b |
Puig Adam, presenta una solución más elegante. Identifica la homología que hay entre el círculo usado y la curva buscada. Se aparta de la simplicidad perseguida en que hay que conocer además el manejo de las homologías.
Sidler usa la polaridad para llegar a una demostración realmente corta; pero entonces debemos ir más allá y debemos introducir la conjugación y la polaridad... |
||
|
En la actualidad, para demostrar los recíprocos, nos basaríamos en la simpleza de los teoremas directos, y por dualidad, los daríamos como demostrados. Esta sería la demostración más corta; pero deberíamos introducir el concepto de dualidad.
Visto lo anterior, estamos seguros que la demostración usada, aunque laboriosa, usa ideas muy próximas a la geometría clásica; pensemos que la razón doble ya la usaba Papus y según él dice también la usaba Apolonio. En cuanto al procedimiento, se obtiene de observar las figuras y sacar a flote las relaciones geométricas que nos son necesarias.
Nota 5 En cuanto al GRAN TEOREMA DE PONCELET ya se ha visto que sencillo aunque sólo se conozcan las primeras propiedades fundamentales de las cónicas.
También se podría haber demostrado recurriendo al teorema de Pascal o de Brianchon; pero si introducimos la involución y la conjugación hay una demostración a partir de este TEOREMA DE DESARGUES (dual del tercer teorema de Desargues):
Las tangentes trazadas desde un punto D a las cónicas de un haz tangencial son homólogas en una involución de D*. Las rectas dobles de dicha involución son tangentes en D a las cónicas del haz tangencial que pasan por este punto.
Sidler, dando por sabido el teorema y sin mencionarlo, resuelve el tema del triángulo en los polígonos cerrados de Poncelet de la siguiente forma:
“Sean ABC y A’‘B’C’ dos triángulos circunscritos a una cónica Γ. Para establecer que los puntos A, B, C, D, A’, B’, C’ pertenecen a una misma cónica Ω, demostramos que la involución δ definida sobre BC por el cuadrángulo AA’B’C’ intercambia la posición de los punto B y C. Basta para ello, verificar que la involución δ es la “proyección” sobre BC de la involución δ* de A*, definida por el haz tangencial de cónicas tangentes a las rectas A’C’, A’B’, B’C’ y BC. La reciproca es la proposición dual. Como corolario si existe un triángulo inscrito a una cónica y circunscrito a otra cónica, existe una infinidad de ellos.”
Nota 6 En el apéndice del problema 137 de las páginas de RICARDO BARROSO obtuvimos la cónica por cinco puntos. En este caso, nos hace falta obtener la cónica por cinco tangentes; pues el problema asegura la existencia de la cónica inscrita y de seis de sus tangentes.
Nota 7 Es deuda a pagar en un futuro. Un método de trazado de la cónica dadas cinco tangentes y una generalización sencilla al caso del polígono de n lados. |
|||