Problema 182.-El teorema de los polígonos cerrados de Poncelet.

Se tienen dos circunferencias una k dentro de otra K. Supongamos que desde un punto A de K (la exterior) sucede lo siguiente: Trazamos por A una tangente a k que vuelve a cortar a K en B; por B trazamos la otra tangente a k, que vuelve a cortar a K en C; por C trazamos la otra tangente a k, que resulta que vuelve a cortar a K en A (es decir, se cierra la sucesión de tres tangentes). Entonces eso mismo pasa (es decir el triángulo también se cierra) cuando hacemos la misma operación partiendo de cualquier otro punto A* de K.

¡Demostrarlo!

(La experiencia de descubrir en Geometría. Miguel de Guzmán, pág. 102).

En el enunciado anterior puede sustituirse la palabra circunferencia(s) por cónica(s) y el enunciado subsiste.

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Vamos a tratar el problema en el caso más general de dos cónicas, para ello comenzaremos dando una definición de cónica proyectiva, siguiendo a D. Pedro Puig Adam en su Geometría Métrica.

Una cónica puntual es el lugar geométrico de los puntos comunes a los pares de rayos homólogos de dos haces proyectivos no perspectivos.

Dualmente podemos definir la cónica tangencial o cónica dual:

Como envolvente de las rectas que unen los pares de puntos homólogos de dos proyectividades (u homografías) entre dos rectas diferentes.

La solución del problema la haremos en dos etapas:

Teorema 1.- Si los seis vértices de dos triángulos están sobre una cónica, los seis lados de los triángulos son tangentes a otra cónica y viceversa. (Frank Ayres, Geometría Proyectiva, Mac Graw Hill, pág. 98.)

Demostración

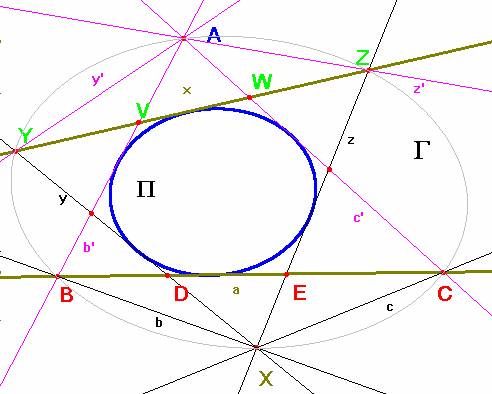
Consideremos la cónica G de la figura en la que se encuentran los triángulos ABC y XYZ como generada por los haces de rectas de vértices los puntos A y X. La correspondencia (homografía o proyectividad) entre estos haces es:

b=XB à b’= AB ; c = XC à c’= AC; y =XY à y’= AY (y también z = XZ à z’= AZ).

Esta correspondencia entre los haces de rectas define una proyectividad entre las rectas a y x sin más que cortar el haz de vértice X con a y el de vértice A con x.

(B, D, E, C) à (V, Y, Z, W)

Ahora bien, esta correspondencia entre estos «haces de puntos», define una cónica tangencial P: la definida por las rectas que unen cada punto con su homólogo, es decir, la cónica que tiene como tangentes las rectas b’=BV; y=DY; z=EZ; c’=CW y las rectas base de la homografía x=YZ, y a=BC, con lo cual se demuestra el teorema.

Teorema 2 (De los polígonos cerrados de Poncelet).- Si hay un triángulo inscrito en una cónica y circunscrito a una segunda cónica, entonces existen infinitos triángulos con esa propiedad, eligiendo un punto arbitrario de la cónica exterior como vértice.

Sea ABC el triángulo dado (circunscrito a P e inscrito en G). Desde un punto X de la cónica circunscrita trazo las tangentes a P, XY y XZ. Los triángulos ABC y XYZ son ambos inscritos en la cónica G, y por el teorema 1 , sus lados son tangentes a otra cónica P. Cinco de los lados AB, AC, BC, XY y XZ determinan unívocamente esa cónica, por tanto YZ ha de ser también tangente a P. c.q.d.