Propuesto por Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

Problema 183

Dado un triángulo ABC y una transversal t, se toma un punto cualquiera de ella V y se trazan rectas VA, VB y VC. Se toman después rectas VA', VB' y VC' simétricas de las primeras respecto de la transversal t, siendo A', B' y C' los puntos de intersección con los lados BC, CA y AB del triángulo.

Demostrar que A', B' y C' están alineados.

Campo, S. (2004): Comunicación personal

Solución de José María Pedret, Ingeniero Naval. Esplugues de Llobregat (Barcelona)

0.

INTRODUCCION

Procedimiento general.

Los problemas de triángulos relacionados con rectas (transversales), que no pasan por sus vértices, y los problemas de triángulos relacionados con puntos, que no están sobre sus lados, presentan multitud de aspectos interesantes.

Si en relación con este tipo de problemas, debemos establecer una concurrencia de rectas o un alineamiento de puntos, el tratamiento más general es usar el SEGUNDO TEOREMA DE DESARGUES, adaptar este teorema en lugar de  a un cuadrángulo a un triángulo y ser capaces de escribir sus teoremas duales.

Una vez hecho lo anterior, se particulariza a las condiciones del enunciado propuesto y se establece el resultado.

Conocimientos supuestos.

*

*

*

*

*

*

*

Referencia proyectiva,

recta proyectiva y haz de rectas,

razón doble de cuatro puntos alineados y de cuatro rectas de un haz,

homografía entre rectas y  entre haces,

puntos fijos de una homografía de una recta sobre sí misma y rayos dobles de una homografía de un haz sobre sí mismo,

idea práctica de la dualidad en dimensión 1,

definición de un cuadrángulo y un cuadrilátero.

Como la gracia de este teorema de Desargues está en las involuciones, estableceremos lo necesario de ellas durante el desarrollo.

1.

LAS INVOLUCIONES

Definición

Se dice que una homografía σ : r → r de una recta proyectiva sobre sí misma es una INVOLUCION si es distinta de la identidad y si (σ ◦ σ) es la aplicación idéntica de r (es decir σ^-1 = σ).

Si σ es una involución, entonces P' = σ(P) y P = σ(P'). Se dice que la involución intercambia los puntos P y P' o que P y P' son puntos homólogos en la involución.

Proposición básica

Una homografía σ : r → r de una recta proyectiva sobre sí misma es una INVOLUCION si y sólo si ∃ P ∈ r ∕ σ(P) ≠ P y σ(σ(P)) = P.

Demostración de la proposición básica

La parte directa es la propia definición.

Para la recíproca tomemos P ≠ P' con P ∈ r, P' ∈ r ∕ P' = σ(P), P = σ(P'). ∀ Q ∈ r ∕ Q ≠ P, Q ≠ P', si ponemos Q' = σ(Q) basta demostrar que Q = σ(Q'). Atendiendo a la conservación de las razones doble en la homografía, tenemos:

(P, P', Q, Q') = (σ(P), σ(P'), σ(Q), σ(Q')) = (P', P, Q', σ(Q')) = (P, P', σ(Q'), Q') ⇒ σ(Q') = Q.

Teorema 1

Sean A, B ∈ r ∕ A ≠ B. Entonces la involución σ : r → r, que admite a A, B como puntos fijos, es única. ∀ P ∈ r ∕ P ≠ A, P ≠ B, se tiene:

(A, B, P, σ(P)) = -1.

Recíprocamente, esta relación define una involución de puntos fijos A y B.

Demostración del teorema 1

Existencia:

Unicidad:

Sea C ∈ r ∕ C ≠ A, C ≠ B y sea C' ∈ r ∕ (A, B, C, C') = -1. La homografía σ : r → r definida por σ(A) = A , σ(B) = B  y   σ(C) = C' es una involución. Como σ conserva la razón doble ρ, escribimos:

1/ρ = (A, B, C, C') = (σ(A), σ(B), σ(C), σ(C')) = (A, B, C', σ(C')) = -1/-1 = -1,

1/ρ = (A, B, C', C) = (σ(A), σ(B), σ(C'), σ(C)) = (A, B, σ(C'), C') = -1/-1 = -1,

Entonces (A, B, C, C') = -1 = (A, B, σ(C'), C') ⇒ σ(C') = C

∀ P ∈ r ∕ P ≠ A, P ≠ B, tenemos:

ρ = (A, B, P, σ(P)) = (σ(A), σ(B), σ(P), σ(σ(P))) = (A, B, σ(P), P) = 1/ρ ⇒ ρ² = 1;

pero ρ ≠1 ⇒ ρ = -1 y por tanto σ(P) es único.

Teorema 2

Sean A ∈ r, A'∈ r, B ∈ r, B'∈ r ∕ {A,A'} ∩ {B,B'} = Ø, ∃ σ : r → r (única) ∕ σ(A) = A' y σ(B) = B'.

Demostración del teorema 2

Caso A ≠ A':

Caso B ≠ B':

A = A', B = B':

Entonces A, A', B forman una referencia proyectiva de la recta r. Existe entonces una única homografía σ : r → r definida por σ(A) = A', σ(B) = B', σ(A') = A. Esta homografía, gracias a la proposición básica, es una involución.

Análogo al caso A ≠ A'.

Nada que demostrar, pues es el caso de dos puntos fijos (teorema 1).

2.

USO DE LA DUALIDAD

Receta en el caso de dimensión 1

Podemos escribir las formas duales de los enunciados precedentes sin más que hacer los siguientes cambios:

punto por recta

recta por punto

puntos alineados por rectas concurrentes

rectas concurrentes por puntos alineados

cuadrángulo por cuadrilátero

cuadrilátero por cuadrángulo

Como muestra podemos ver la “dualización” del teorema 1.

Teorema 3. (Dual del teorema 1)

Sean a, b dos rectas concurrentes en un punto R. Entonces la involución del rectas σ* : R* → R*, que admite a a, b como rectas fijas, es única. ∀ r ∈ R* ∕ r ≠ a, r ≠ b, se tiene:

(a, b, r, σ(r)) = -1.

Ventajas del dual

Podemos usar lo establecido y demostrado para puntos de rectas proyectivas con las rectas de un haz. Basta sólo con “dualizar” los enunciados.

3.

EL SEGUNDO TEOREMA DE DESARGUES

Demostraremos el segundo teorema de Desargues con el uso de esta proposición previa:

Teorema 4. (Previo al Segundo teorema de Desargues)

Sean A₁, A₂, A₃ y A'₁, A'₂, A'₃ dos referencias de la recta proyectiva. Una homografía σ : r → r definida por σ(A_i) = A'_i es una involución si y sólo si se tiene la igualdad (A₁, A₂, A₃, A'_i) = (A'₁, A'₂, A'₃, A_i) para al menos un índice i ∈ {1, 2, 3}.

Demostración del teorema 4. (Jean-Claude Sidler)

A₁, A₂, A₃, A'_i

distintos:

A₁, A₂, A₃, A'_i

no distintos:

Si la homografía es una involución, las tres razones dobles son iguales. Recíprocamente si tenemos:

ρ = (A₁, A₂, A₃, A'_i)                     = (A'₁, A'₂, A'₃, A_i)       

ρ = (σ(A₁), σ(A₂), σ(A₃), σ(A'_i)) = (A'₁, A'₂, A'₃, σ(A'_i)).

De donde se deduce que σ(A'_i) = A_i.

Se trata directamente.

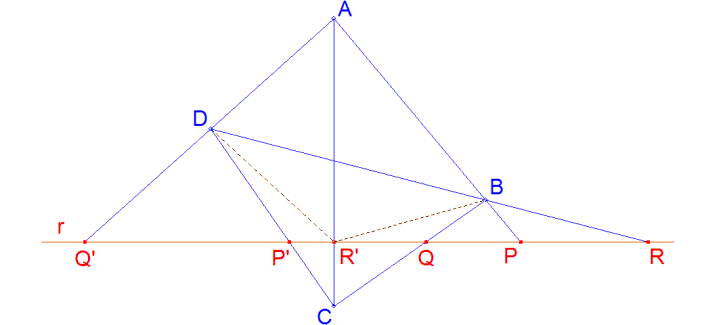
Teorema 5. (Segundo teorema de Desargues).

Sea un cuadrángulo ABCD y sea r una recta que no pasa por ninguno de sus vértices. Los lados opuestos del cuadrángulo cortan a r en puntos que se corresponden en una misma involución.

Demostración del teorema 5

Los tres pares de lados opuestos son (AB, CD), (BC, DA), (AC, DB).

Para demostrar que AB ∩ r = P, CD ∩ r = P', BC ∩ r = Q, DA ∩ r = Q', AC ∩ r = R, DB ∩ r = R' son homólogos en una misma involución, utilizaremos el teorema anterior (teorema 4). Nos bastará demostrar:

(P, Q, R, R') = (P', Q', R', R).

Para ello proyectamos r sobre AC con centro de proyección en B y luego AC sobre r con centro de proyección en D. Como las proyecciones conservan la razón doble, basta observar la figura para escribir:

(P, Q, R, R') = (BA, BC, BD, BR') = (DA, DC, DB, DR') = (Q', P', R, R')

4.

ENUNCIADO DEL SEGUNDO TEOREMA DE DESARGUES ADAPTADO A TRIANGULOS

Teorema 6. (Segundo teorema de Desargues adaptado para triángulos).

Un triángulo ABC es cortado por una recta s que no pasa por ninguno de sus vértices según BC ∩ s = P, CA ∩ s = Q, AB ∩ s = R. Tres rectas p, q, r pasando respectivamente por A, B, C cortan a s en P', Q', R'. En estas condiciones, las rectas p, q, r son concurrentes si y sólo si los puntos P y P', Q y Q', R y R' son homólogos en una misma involución.

Demostración del teorema 6 para triángulos.

Si suponemos que p, q, r concurren en D, basta aplicar el segundo teorema de Desargues (teorema 5) al cuadrángulo ABCD. Recíprocamente si los puntos P y P', Q y Q', R y R' son homólogos en una misma involución σ : s → s las rectas p, q, r son concurrentes. En efecto, sea el punto D = p ∩ q; sea R" = CD ∩ s. Después de la parte directa del teorema, los pares de puntos (P, P'), (Q, Q'), (R, R") son homólogos en una misma involución; pero esta involución no es otra que σ, pues hemos visto en el teorema 2 que una involución queda definida por dos pares de puntos homólogos. Tenemos entonces R" = R' = σ(R) y la recta DC coincide con r.

5.

ENUNCIADOS DUALES DEL SEGUNDO TEOREMA DE DESARGUES

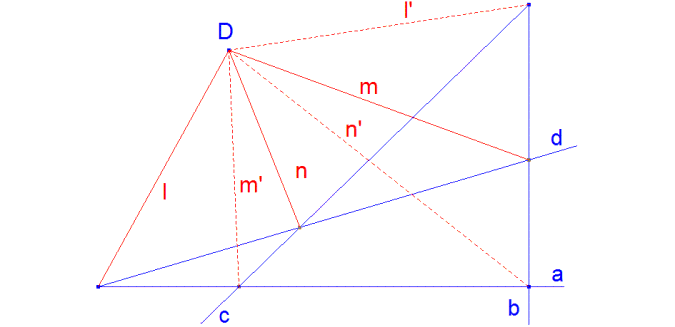
Teorema 7. (Dual del segundo teorema de Desargues para el cuadrilátero. Dual del teorema 5)

Sea abcd un cuadrilátero completo y D no situado sobre los lados del cuadrilátero. Los tres pares de rectas que unen D a los tres pares de vértices opuestos son homólogas en una misma involución del haz de rectas D*.

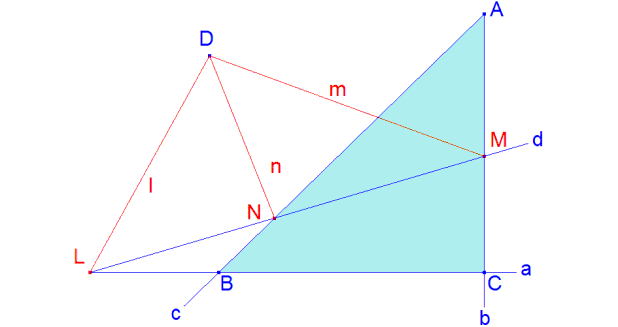
Teorema 8. (Dual del segundo teorema de Desargues para el triángulo. Dual del teorema 6)

Sea un triángulo ABC y un punto D no situado sobre los lados a = BC, b = AC, c = AB de dicho triángulo. Sean l. m. n tres rectas de D* que cortan a a, b, c en L, M, N. Los puntos L, M, N están alineados si y sólo si la homografía de σ* : D* → D* definida por σ(l) = DA, σ(m) = DB, σ(n) = DC es una involución.

6.

CONCLUSION (RESOLUCION DEL ENUNCIADO INICIAL)

Para demostrar el enunciado basta tomar D = V, L = A', M = B', N = C'y aplicar el dual del segundo teorema de Desargues para el triángulo. Considerando la involución (simetría axial respecto la recta transversal t) definida como:

σ* : V* → V* con σ(VA') = VA, con σ(VB') = VB, con σ(VB') = VB, (la simetría axial es involución; σ(σ(VA')) = σ( VA) = VA'),

Entonces A', B' C' están alineados.