Problema 187:
Supongamos que las cevianas AD, BE y CF tienen un punto P común en el interior de ABC. Demostrar que DP/AD + EP/BE + FP/CF =1
Rike, T. (2003) Perennial problems from geometry. Berkeley math circle.
Demostración: Juan Carlos Salazar, Profesor de Geometría del Equipo Olímpico de Venezuela.(Puerto Ordaz) (12 de julio de 2004).
Ver Fig. 1
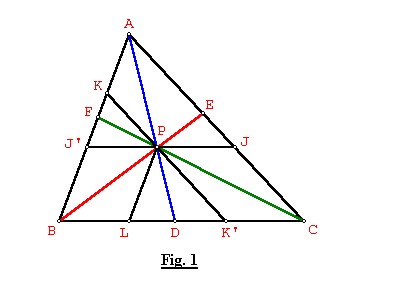
Desde el punto P trazamos los segmentos PL, PJ, PK con L, J, K sobre los lados BC, AC, AB respectivamente, de tal manera que PL//AB, PJ//BC, PK//AC.
Así tenemos que los pares de triángulos (PLD, ABD); (PJE, EBC); (PKF, AFC) son semejantes entre sí. Por consiguiente:
Para los triángulos PLD y ABD:
DP/AD = PL/AB... (1)
Para los triángulos PJE y EBC:
EP/BE = PJ/BC... (2)
Para los triángulos PKF y AFC:
FP/CF = PK/AC... (3)
Sumando (1), (2) y (3):
DP/AD + EP/BE + FP/CF = PL/AB + PJ/BC + PK/AC …..(I)
A continuación probaremos que: PL/AB + PJ/BC + PK/AC = 1
Como al prolongar KP hasta K' en BC se cumple que: PJ = K'C, ya que el cuadrilátero PK'CJ es un paralelogramo, de manera similar al prolongar JP hasta J' en AB, se logra: J'P =BL y además los triángulos PLK', KJ'P y ABC son semejantes.
Luego tenemos que:
PL/AB + PJ/BC + PK/AC = LK'/BC + K'C/BC + J'P/BC = LK'/BC + K'C/BC + BL/BC
PL/AB + PJ/BC + PK/AC = (BL + LK' + K'C)/BC = BC/BC = 1
Reemplazando en (I):
DP/AD + EP/BE + FP/CF = 1 QED.
Juan Carlos Salazar