Problema 188: Punto de Clawson.

Dado un triángulo acutángulo ABC, consideremos dos triángulos:

a) El órtico, Ha Hb Hc

b) El triángulo MNP, formado por las tangentes exteriores al conjunto de los tres círculos

exinscritos al triángulo ABC.

Los triángulos Ha Hb Hc y MNP son homotéticos y su centro de homotecia es el punto de Clawson.

Solución:

Consideramos la configuración completa, donde tenemos las tangentes interiores y exteriores a los excírculos del triángulo ABC (Ver Fig. 1).

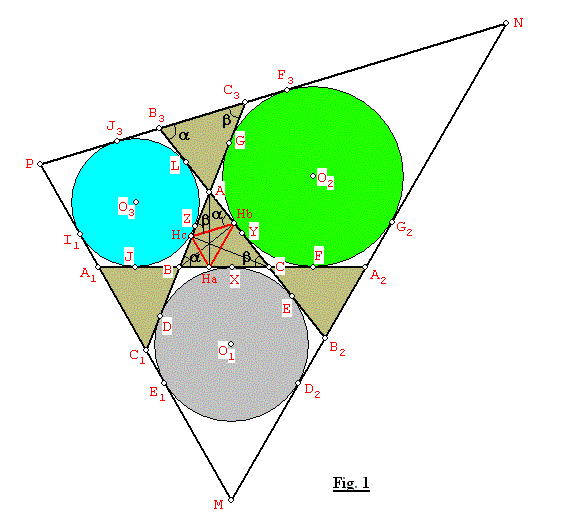
Los cuatro triángulos ABC, AB₃C₃, BA₁C₁ y CB₂A₂ conformados por las tangentes son congruentes, debido a que los pares de triángulos: ABC y AB₃C₃, ABC y BC₁A₁, ABC y CB₂A₂ son simétricos con respecto a las rectas O₂O₃, O₁O₃ y O₁O₂ respectivamente.

Sabemos que los triángulos AHbHc, BHaHc, CHbHa y ABC son semejantes, además tenemos por ejemplo: <B = <HcHbA = a y <C = <AHcHb = b, también: <AB3= <HcHbA = a y <AC₃B₃ = <AHcHb = b, es decir que HcHb // B₃C₃//PN, de manera similar podemos probar que HaHc//A₁C₁//PM y HaHb//A₂B₂//MN.

Por lo tanto podemos concluir que los triángulos HaHbHc y MNP tienen sus lados correspondientemente paralelos y desde luego por este hecho son homotéticos. Al centro de homotecia de estos dos triángulos se le denomina punto de Clawson del triángulo ABC. QED.

Juan Carlos Salazar

caisersal@yahoo.com