Problema 188.- Punto de Clawson.

Dado un triángulo acutángulo ABC, consideremos dos triángulos:

a) El órtico, A*B*C* .

b) El triángulo MNP, formado por las tangentes exteriores al conjunto de los tres círculos exinscritos al triángulo ABC.

c) Los triángulos A* B* C* y MNP son homotéticos y su centro de homotecia es el punto de Clawson. http://mathworld.wolfram.com/ClawsonPoint.html .

Solución de Saturnino Campo Ruiz, profesor del IES Fray Luis de León, de Salamanca

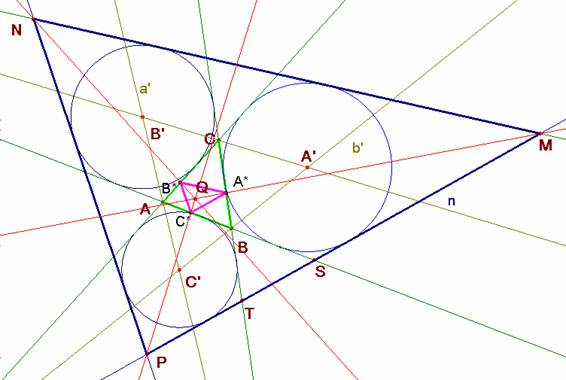
La recta b’= A’C’, además de ser la bisectriz exterior de B es la bisectriz (interior) de las rectas b=AC y n=PM por tanto, una simetría de eje esta recta b’ transforma b=AC en n=PM ; c=AB en a=BC y viceversa. Para los puntos de intersección se tienen: A → T y C → S

En consecuencia los triángulos ABC y TBS son iguales.

En el triángulo A*BC* (ver problema nº 17 propiedades del triángulo órtico A*B*C*) tenemos áng (C*A*B) = áng (CAB)= áng (STB), de lo que se deduce que los lados C*A* y MP son paralelos, e igualmente para el resto de los lados.

Si los triángulos A*B*C* y MNP tienen sus lados paralelos son homotéticos y Q, el centro de esa homotecia, es el punto de Clawson.

c.q.d.